A road network as shown in the figure connect four cites. In how many ways can you start from any city (say A) and come back to it without travelling on the same road more than once ?
To solve the problem of how many ways we can start from city A and return to it without traveling on the same road more than once, we will analyze the road network step by step.
1. Identify the Cities and Roads:
Let's denote the cities as A, B, C, and D. The roads connecting these cities are as follows:
- A to B
- A to C
- A to D
- B to C
- B to D
- C to D
2. Starting from City A:
We can start our journey from city A. From A, we have three options to travel to:
- B (via road AB)
- C (via road AC)
- D (via road AD)
3. Choosing the First Road:
Let's consider each option:
- If we go to B, we can then go to either C or D.
- If we go to C, we can then go to either B or D.
- If we go to D, we can then go to either B or C.
4. Calculating Paths from Each City:
- From A to B:
- From B, we can go to C or D.
- If we go to C (B to C), we can then go back to A (via AC) or go to D (B to C to D).
- If we go to D (B to D), we can then go back to A (via AD) or go to C (B to D to C).
- From A to C:
- From C, we can go to B or D.
- If we go to B (C to B), we can then go back to A (via AB) or go to D (C to B to D).
- If we go to D (C to D), we can then go back to A (via AD) or go to B (C to D to B).
- From A to D:
- From D, we can go to B or C.
- If we go to B (D to B), we can then go back to A (via AB) or go to C (D to B to C).
- If we go to C (D to C), we can then go back to A (via AC) or go to B (D to C to B).
5. Counting the Total Paths:
- From A to B:
- B to C (2 choices: back to A or to D)
- B to D (2 choices: back to A or to C)
- Total from A to B: 2 + 2 = 4 ways.
- From A to C:
- C to B (2 choices: back to A or to D)
- C to D (2 choices: back to A or to B)
- Total from A to C: 2 + 2 = 4 ways.
- From A to D:
- D to B (2 choices: back to A or to C)
- D to C (2 choices: back to A or to B)
- Total from A to D: 2 + 2 = 4 ways.
6. Final Calculation:
Since we have 3 choices to start from A (to B, C, or D), and each choice leads to 4 unique paths, the total number of ways to start from A and return to A without traveling the same road more than once is:
Total Ways=3×4=12
Conclusion:
Thus, the total number of ways to start from city A and return to it without traveling on the same road more than once is 12.
Let's denote the cities as A, B, C, and D. The roads connecting these cities are as follows:
- A to B
- A to C
- A to D
- B to C
- B to D
- C to D
We can start our journey from city A. From A, we have three options to travel to:
- B (via road AB)
- C (via road AC)
- D (via road AD)
Let's consider each option:
- If we go to B, we can then go to either C or D.
- If we go to C, we can then go to either B or D.
- If we go to D, we can then go to either B or C.
- From A to B:
- From B, we can go to C or D.
- If we go to C (B to C), we can then go back to A (via AC) or go to D (B to C to D).
- If we go to D (B to D), we can then go back to A (via AD) or go to C (B to D to C).
- From A to C:
- From C, we can go to B or D.
- If we go to B (C to B), we can then go back to A (via AB) or go to D (C to B to D).
- If we go to D (C to D), we can then go back to A (via AD) or go to B (C to D to B).
- From A to D:
- From D, we can go to B or C.
- If we go to B (D to B), we can then go back to A (via AB) or go to C (D to B to C).
- If we go to C (D to C), we can then go back to A (via AC) or go to B (D to C to B).
- From A to B:
- B to C (2 choices: back to A or to D)
- B to D (2 choices: back to A or to C)
- Total from A to B: 2 + 2 = 4 ways.
- From A to C:
- C to B (2 choices: back to A or to D)
- C to D (2 choices: back to A or to B)
- Total from A to C: 2 + 2 = 4 ways.
- From A to D:
- D to B (2 choices: back to A or to C)
- D to C (2 choices: back to A or to B)
- Total from A to D: 2 + 2 = 4 ways.
Since we have 3 choices to start from A (to B, C, or D), and each choice leads to 4 unique paths, the total number of ways to start from A and return to A without traveling the same road more than once is:
Total Ways=3×4=12
Thus, the total number of ways to start from city A and return to it without traveling on the same road more than once is 12.
Topper's Solved these Questions
Similar Questions
There are five cities A, B, C, D, E on a certain island. Each city is connected to every other city by road. In how many ways can a person starting from city A come back to A after visiting some cities without visiting a city more than once and without taking the same road more than once ? (The order in which he visits the cities also matters. e.g., the routes A→B→CAandA→C→B→A are different).
View SolutionHow many numbers of 5 digits can be formed with the digit 0,2,5,6,7 without taking any of these digit more than once.
View SolutionFrom a committee of 8 persons, in how many ways can we choose a chairman and a vice chairman assuming one person cannot hold more than one position?
View SolutionA car is travelling on a road. The maximum velocity the car can attain is 24ms−1 and the maximum deceleration is 4ms−2. If car starts from rest and comes to rest after travelling 1032m in the shortest time of 56 s, the maximum acceleration that the car can attain is
View SolutionHow many even numbers of four digits can be formed with the digits 0,1,2,3,4,5 and 6 no digit being used more than once?
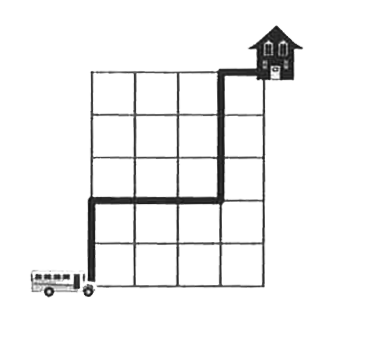
View SolutionEvery moring, Grishma walks from her house to the bus stop , the placement of the house and bus stop are shown in the diagram to the right. She always travels exactly nine blocks from her house to the bus, but she varies the route she takes every day. (One sample route is shown.) How many days can Grishma walk from her house to the bus stop without repeating the same route?
View SolutionA bag contains four one-rupee coins, two twenty-five paisa coins, and five ten-paisa coins. In how many ways can an amount, not less than Rs. 1 be taken out from the bag? (Consider coins of the same denominations to be identical.) a. 71 b. 72 c. 73 d. 80
View SolutionA man has 8children to take them to a zoo. He takes thre of them at a time to the zoo as often as he can without taking the same 3 children together more than once. How many times will he have to go to the zoo? How many times a particular child will to to the zoo?
View SolutionA small ring of mass m is constrained to slide along a horizontal wire fixed between two rigid supports. The ring is connected to a particle of same mass by an ideal string & the whole system is released from rest as shown in the figure. If the coefficient of friction between ring A and wire is 35, the ring will start sliding when the connecting string will make an angle θ with the vertical, then θ will be (particle is free to move and ring can slide only)

View SolutionA van is standing on a frictionless portion of a horizontal road. To start the engine, the vehicle must be set in motion in theforward direction. How can the persons sitting inside the van do it without coming out and pushing from behind?
View Solution
