If f(a,b)=f(b)−f(a)b−a and
f(a,b,c)=f(b,c)−f(a,b)c−a prove that f(a,b,c)=∣∣
∣
∣∣f(a)f(b)f(c)111abc∣∣
∣
∣∣÷∣∣
∣
∣∣111abca2b2c2∣∣
∣
∣∣.
Step by step video & image solution for If f(a,b)=(f(b)-f(a))/(b-a) and f(a,b,c)=(f(b,c)-f(a,b))/(c-a) prove that f(a,b,c)=|{:(f(a),f(b),f(c)),(1,1,1),(a,b,c):}|-:|{:(1,1,1),(a,b,c),(a^(2),b^(2),c^(2)):}|. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
If f(x)=ax2+bx+candf(x+1)=f(x)+x+1, then the value of (a+b) is __
A-2B-1C0D1
f(x)=xx−1 then f(a)f(a+1) is equal to a.f(−a) b.f(1/a) c.f(a2) d.f(−aa−1)
View SolutionUsing properties of determinant, If f(x)=a+bx+cx2, prove that ∣∣ ∣∣abcbcacab∣∣ ∣∣=−f(1)f(ω)f(ω2),ω is a cube root of unity
View SolutionIf g(x)=f(x)(x−a)(x−b)(x−c),where f(x) is a polynomial of degree <3 , then ∫g(x)dx=∣∣ ∣ ∣∣1af(a)log|x−a|1bf(b)log|x−b|1cf(c)log|x−c|∣∣ ∣ ∣∣÷∣∣ ∣ ∣∣1aa21bb21cc2∣∣ ∣ ∣∣+k dg(x)dx=∣[1,a,−f(a)(x−a)−2],[1,b,−f(b)(x−b)−2],[1,c,−f(c)(x−c)−2]∣∣ ∣ ∣∣−∣∣ ∣ ∣∣1aa21bb21cc2∣∣ ∣ ∣∣
View SolutionSuppose we define integral using the following formula ∫baf(x)dx=b−a2(f(a)+f(b)), for more accurate result for c∈(a,b),F(c)=c−a2(f(a)+f(c))+b−c2(f(b)+f(c)).
When c=a+b2, then ∫baf(x)dx=b−a4(f(a)+f(b)+2f(c)).
limt→a∫taf(x)dx−(t−a)2(f(t)+f(a))(t−a)3=0∀a Then the degree of f(x) can at most be
View SolutionSuppose we define integral using the following formula ∫baf(x)dx=b−a2(f(a)+f(b)), for more accurate result for c∈(a,b),F(c)=c−a2(f(a)+f(c))+b−c2(f(b)+f(c)).
When c=a+b2, then ∫baf(x)dx=b−a4(f(a)+f(b)+2f(c)).
limt→a∫taf(x)dx−(t−a)2(f(t)+f(a))(t−a)3=0∀a Then the degree of f(x) can at most be
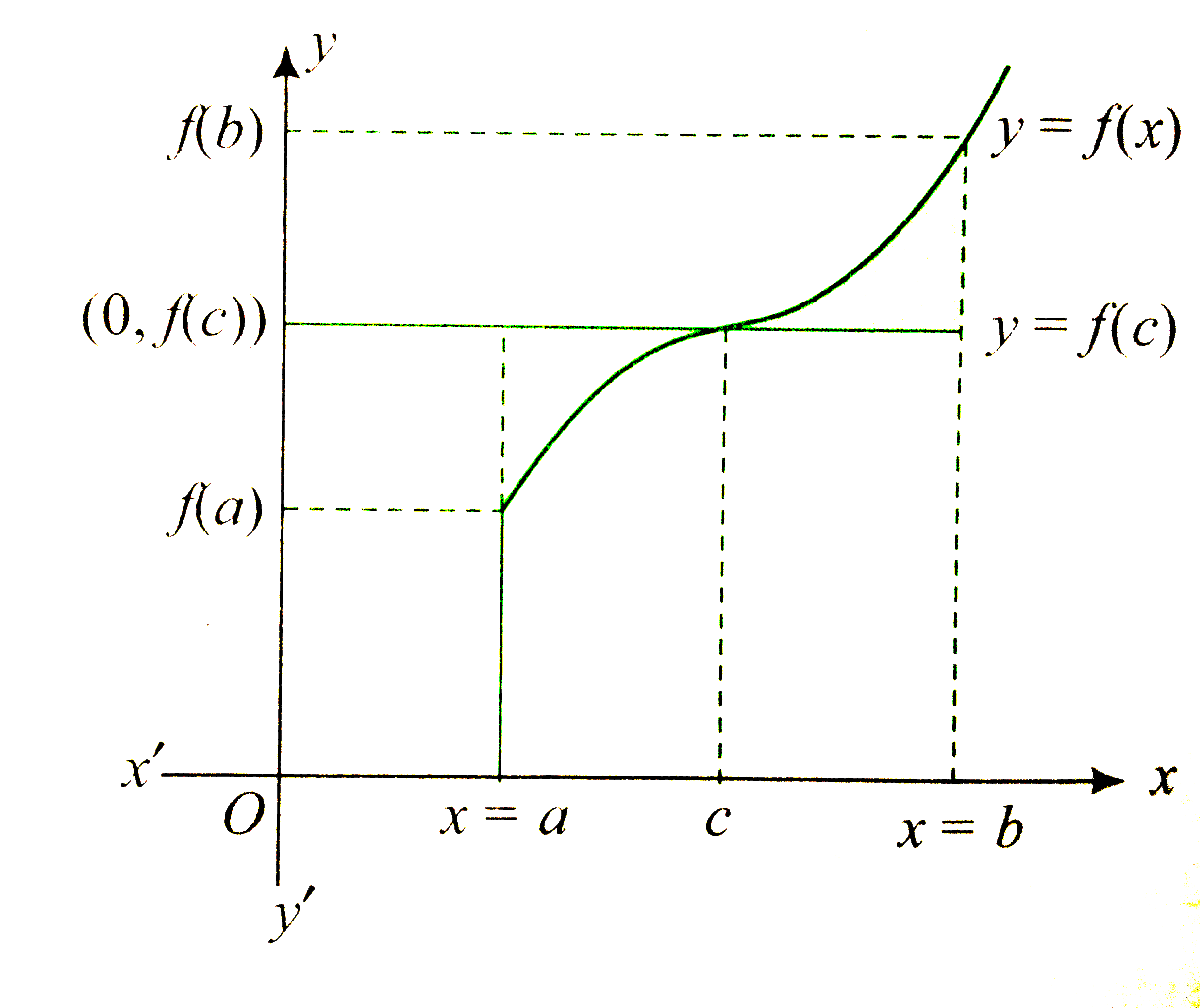
View SolutionIf y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at x=a,x=b,y=f(x)andy=f(c)(where c∈(a,b)) is minimum when c=a+b2.
Proof : A=∫ca(f(c)−f(x))dx+∫bc(f(c))dx
=f(c)(c−a)−∫ca(f(x))dx+∫ba(f(x))dx−f(c)(b−c)
⇒ A=[2c−(a+b)]f(c)+∫bc(f(x))dx−∫ca(f(x))dx
Differentiating w.r.t. c, we get
dAdc=[2c−(a+b)]f'(c)+2f(c)+0−f(c)−(f(c)−0)
For maxima and minima , dAdc=0
⇒ f'(c)[2c−(a+b)]=0(asf'(c)≠0)
Hence, c=a+b2
Also for c<a+b2,dAdc<0 and for c>a+b2,dAdc>0
Hence, A is minimum when c=a+b2.
If the area bounded by f(x)=x33−x2+a and the straight lines x=0, x=2, and the x-axis is minimum, then the value of a is
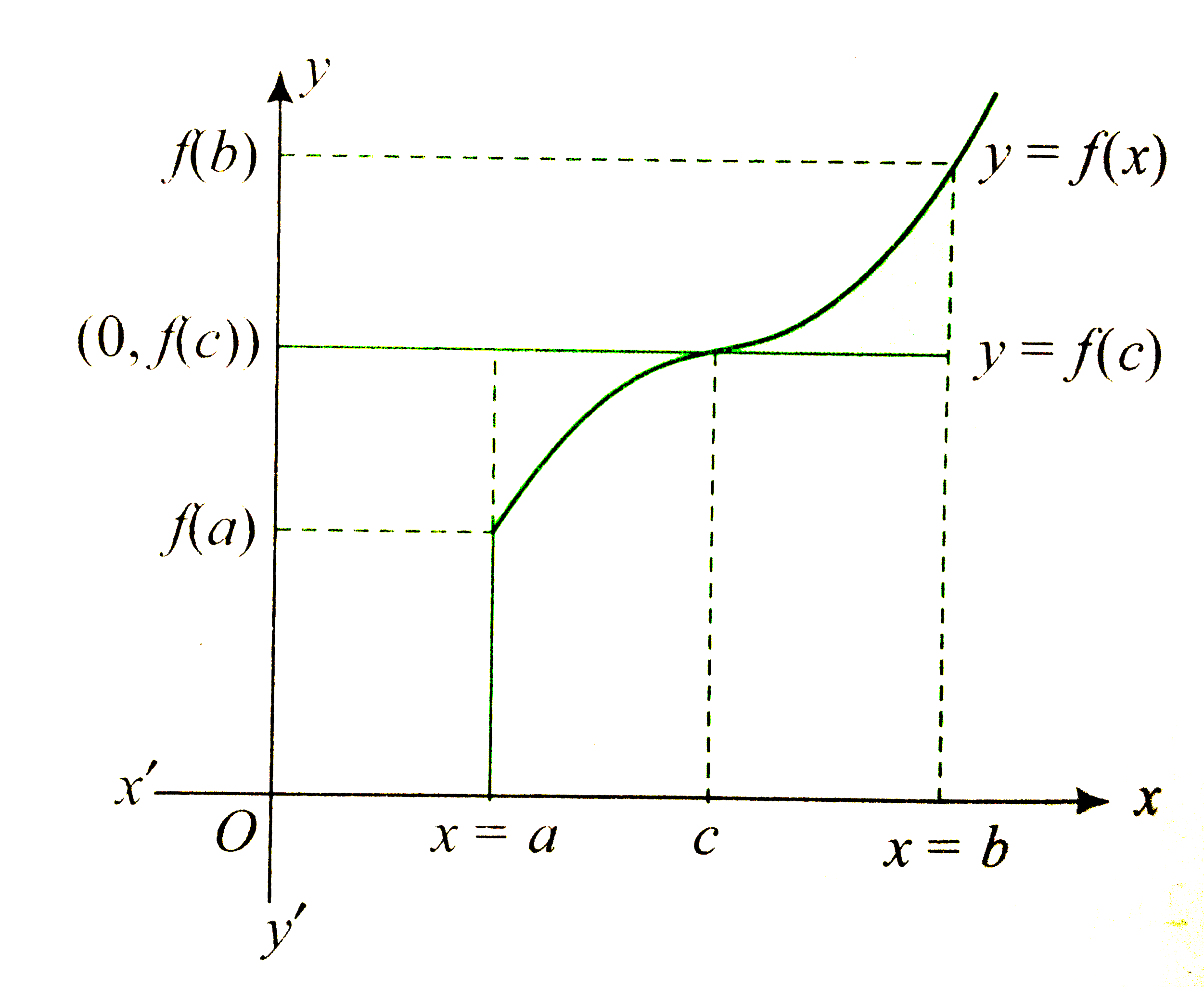
View SolutionIf y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at x=a,x=b,y=f(x)andy=f(c)(where c∈(a,b)) is minimum when c=a+b2.
Proof : A=∫ca(f(c)−f(x))dx+∫bc(f(c))dx
=f(c)(c−a)−∫ca(f(x))dx+∫ba(f(x))dx−f(c)(b−c)
⇒ A=[2c−(a+b)]f(c)+∫bc(f(x))dx−∫ca(f(x))dx
Differentiating w.r.t. c, we get
dAdc=[2c−(a+b)]f'(c)+2f(c)+0−f(c)−(f(c)−0)
For maxima and minima , dAdc=0
⇒ f'(c)[2c−(a+b)]=0(asf'(c)≠0)
Hence, c=a+b2
Also for c<a+b2,dAdc<0 and for c>a+b2,dAdc>0
Hence, A is minimum when c=a+b2.
If the area enclosed by f(x)=sinx+cosx,y=a between two consecutive points of extremum is minimum, then the value of a is
View Solution
