Plot the points in a rectangular coordinate system: (4,5)
To plot the point (4, 5) in a rectangular coordinate system, follow these steps:
1. Draw the Coordinate Axes:
- Begin by drawing two perpendicular lines. The horizontal line represents the x-axis, and the vertical line represents the y-axis. Label the axes accordingly.
2. Mark the Units on the Axes:
- On the x-axis, mark equal intervals. For example, label points as 1, 2, 3, and 4 towards the right of the origin (0,0).
- Similarly, on the y-axis, mark equal intervals. Label points as 1, 2, 3, 4, and 5 upwards from the origin.
3. Locate the x-coordinate:
- Find the x-coordinate of the point, which is 4. Move 4 units to the right from the origin along the x-axis.
4. Draw a Perpendicular Line from the x-coordinate:
- From the point where you marked 4 on the x-axis, draw a vertical line upwards. This line represents the value of the y-coordinate.
5. Locate the y-coordinate:
- Now, find the y-coordinate, which is 5. Move 5 units up from the x-axis along the vertical line you just drew.
6. Draw a Horizontal Line from the y-coordinate:
- From the point where you marked 5 on the y-axis, draw a horizontal line to the left until it intersects with the vertical line you drew from the x-coordinate.
7. Identify the Point:
- The intersection of the vertical line from the x-coordinate (4) and the horizontal line from the y-coordinate (5) is the point (4, 5). Mark this point clearly.
8. Label the Point:
- Finally, label the point as (4, 5) for clarity.
Summary:
You have successfully plotted the point (4, 5) in the rectangular coordinate system.
- Begin by drawing two perpendicular lines. The horizontal line represents the x-axis, and the vertical line represents the y-axis. Label the axes accordingly.
- On the x-axis, mark equal intervals. For example, label points as 1, 2, 3, and 4 towards the right of the origin (0,0).
- Similarly, on the y-axis, mark equal intervals. Label points as 1, 2, 3, 4, and 5 upwards from the origin.
- Find the x-coordinate of the point, which is 4. Move 4 units to the right from the origin along the x-axis.
- From the point where you marked 4 on the x-axis, draw a vertical line upwards. This line represents the value of the y-coordinate.
- Now, find the y-coordinate, which is 5. Move 5 units up from the x-axis along the vertical line you just drew.
- From the point where you marked 5 on the y-axis, draw a horizontal line to the left until it intersects with the vertical line you drew from the x-coordinate.
- The intersection of the vertical line from the x-coordinate (4) and the horizontal line from the y-coordinate (5) is the point (4, 5). Mark this point clearly.
- Finally, label the point as (4, 5) for clarity.
You have successfully plotted the point (4, 5) in the rectangular coordinate system.
Similar Questions
Knowledge Check
The points in the rectangular coordinate plane are transformed in such a way that each point A(x,y) is moved to a point A'(kx,ky). If the distance between a point A and the origin is d, then the distance between the origin and thhe point A' is
AkdBdkCdDkdColumn AIn the rectangular coordinate system shown, points A and E lie on the x-axis, and points B and D lie on the y-axis. Point C is the midpoint of the line AB and point F is the midpoint of the line DEColumn BThe slope of the line ABThe slope of the line DE
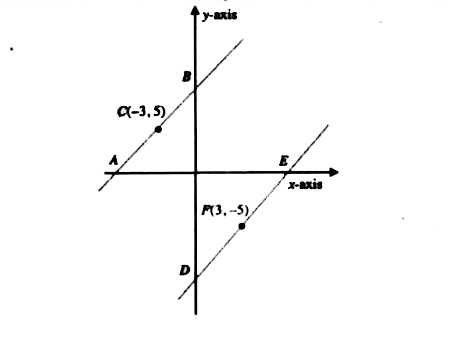 AIf column A is largerBIf column B is largerCIf the columns are equalDIf there is not enough information to decide
AIf column A is largerBIf column B is largerCIf the columns are equalDIf there is not enough information to decide
Plot the points in a rectangular coordinate system: (−2,7)
View SolutionPlot the points in a rectangular coordinate system: (6,−2)
View SolutionPlot the points in a rectangular coordinate system: (−2,−7)
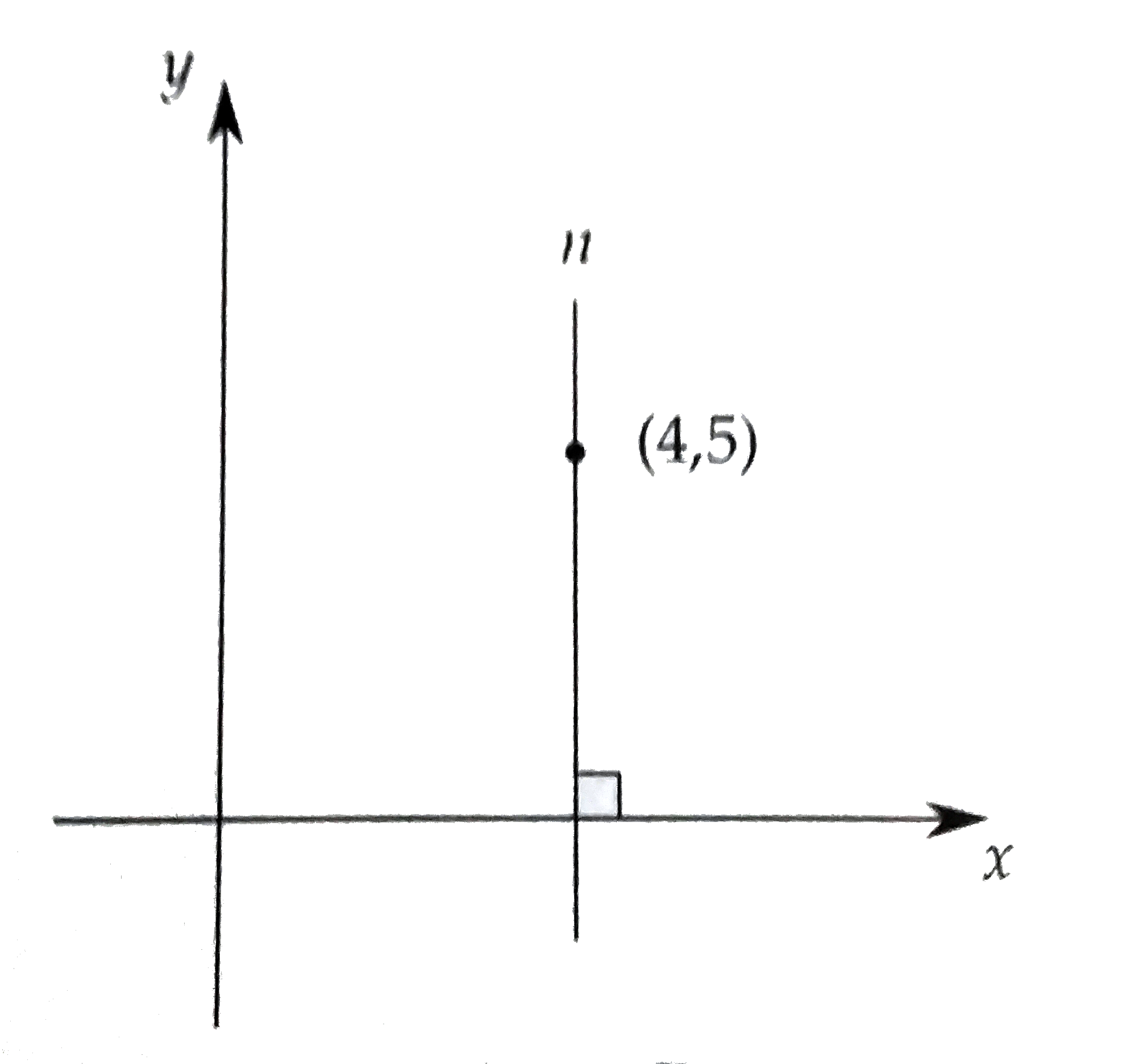
View SolutionFigure shows line n in a rectangular coordinate system. An equation of line n is
View SolutionFind the polar coordinates of the points whose cartesian coordinates are
(−3,4)
View SolutionA point (1, 1) undergoes reflection in the x-axis and then the coordinates axes are rotated through an angle of π4 in anticlockwise direction. The final position of the point in the new coordinate system is
View Solution
