A(a1,b1).B(a2,b2),C(a3,b3) are the vertices of ΔABC. The side AB is divided by the point D in the ratio λ : μ and then the line segment DC is divided by the point E in the ratio u:λ+μ. Find the coordinats of E.
To find the coordinates of point E, we will follow these steps:
Step 1: Find the coordinates of point D
Point D divides the line segment AB in the ratio λ:μ. According to the section formula, the coordinates of point D can be calculated as follows:
D(μa1+λa2λ+μ,μb1+λb2λ+μ)
Step 2: Write down the coordinates of point C
Point C has coordinates (a3,b3).
Step 3: Find the coordinates of point E
Point E divides the line segment DC in the ratio u:(λ+μ). Again, using the section formula, the coordinates of point E can be calculated as follows:
E⎛⎜
⎜⎝u⋅a3+(λ+μ)⋅(μa1+λa2λ+μ)u+(λ+μ),u⋅b3+(λ+μ)⋅(μb1+λb2λ+μ)u+(λ+μ)⎞⎟
⎟⎠
Step 4: Simplify the coordinates of point E
Now, we can simplify the coordinates of point E:
X-coordinate:
Ex=ua3+(λ+μ)(μa1+λa2λ+μ)u+(λ+μ)
This simplifies to:
Ex=ua3+μa1+λa2u+λ+μ
Y-coordinate:
Ey=ub3+(λ+μ)(μb1+λb2λ+μ)u+(λ+μ)
This simplifies to:
Ey=ub3+μb1+λb2u+λ+μ
Final Coordinates of Point E
Thus, the coordinates of point E are:
E(ua3+μa1+λa2u+λ+μ,ub3+μb1+λb2u+λ+μ)
---
Point D divides the line segment AB in the ratio λ:μ. According to the section formula, the coordinates of point D can be calculated as follows:
Point C has coordinates (a3,b3).
Point E divides the line segment DC in the ratio u:(λ+μ). Again, using the section formula, the coordinates of point E can be calculated as follows:
⎜⎝u⋅a3+(λ+μ)⋅(μa1+λa2λ+μ)u+(λ+μ),u⋅b3+(λ+μ)⋅(μb1+λb2λ+μ)u+(λ+μ)⎞⎟
⎟⎠
Now, we can simplify the coordinates of point E:
Ex=ua3+(λ+μ)(μa1+λa2λ+μ)u+(λ+μ)
This simplifies to:
Ex=ua3+μa1+λa2u+λ+μ
Ey=ub3+(λ+μ)(μb1+λb2λ+μ)u+(λ+μ)
This simplifies to:
Ey=ub3+μb1+λb2u+λ+μ
Thus, the coordinates of point E are:
E(ua3+μa1+λa2u+λ+μ,ub3+μb1+λb2u+λ+μ)
Similar Questions
Knowledge Check
If the line joining A(1,3,4) and B is divided by the point (-2,3,5) in the ratio 1:3 then the coordinates of B is
A(−11,3,8)B(−11,8,3)C(11,−8,3)D(−11,−3,8)If point C(−4,1) divides the line segment joining the point A(2,−2) and B in the ratio 3:5, then the coordinates of B are
A(a) (−14,6)B(b) (6,−14)C(c) (−14,−6)D(d) (−6,−14)
If the point C(−1,2) divides internally the line segment joining A(2,5) and B in ratio 3:4, find the coordinates of B.
View SolutionIf point P(3,2) divides the line segment AB internally in the ratio of 3:2 and point Q(−2,3) divides AB externally in the ratio 4:3 then find the coordinates of points A and B.
View SolutionThe line segment joining the points A(3,2) and B (5,1) is divided at the point P in the ratio 1:2 and it lies on the line 3x−18y+k=0. Find the value of k.
View SolutionFind the ratio in which the x - axis divide the line segment joining the point A(2,4)andB(−4,3).
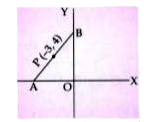
View SolutionIn the figure given below , the line segment AB meets X-axis at A and Y-axis at B. The point P (-3, 4) on AB divides it in the ratio 2:3. Find the coordinates of A and B.
View SolutionA line perpendicular to the in segment joining the points (1,0) and (2,3) divides it in the ratio 1:n . Find the equation of the line.
View Solution
