Two equal parabolas have the same vertex and their axes are at right angles. Prove that their common tangent touches each at the end of their latus recta.
Step by step video & image solution for Two equal parabolas have the same vertex and their axes are at right angles. Prove that their common tangent touches each at the end of their latus recta. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Two equal parabolas have the same vertex and their axes are at right angles. The length of the common tangent to them, is
View SolutionTwo equal parabola have the same vertex and their axes are at right angles. Prove that they cut again at an angle tan−134.
View SolutionTwo identical coils carry equal currents have a common centre and their planes are at right angles to each other. The ratio of the magnitude of the resulatant magnetic field at the centre and the field due to one coil is
View SolutionTwo parabolas with a common vertex and with axes along x-axis and y-axis respectively, intersect each other in the first quadrant. If the length of the latus rectum of each parabola is 3, then the equation of the common tangent to the two parabolas is:
View SolutionIn Figure, two circles touch each other at the point C . Prove that the common tangent to the circles at C , bisects the common tangent at P and Q .
View SolutionIn the figure, two circles touch each other at the point C.Prove that the common tangents to the circles at C, bisect the common tangents at P and Q.
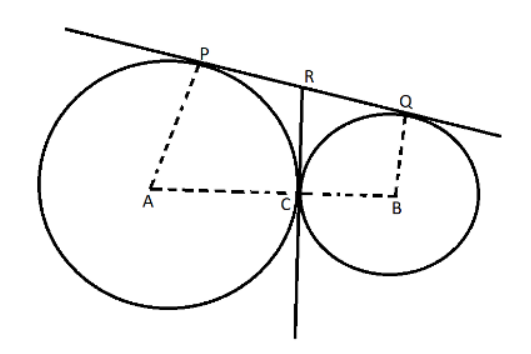
View SolutionTwo diameters of a circle intersect each other at right angles. Prove that the quadrilateral formed by joining their end-points is a square.
View SolutionTwo diameters of a circle intersect each other at right angles. Prove that the quadrilateral formed by joining their end-points is a square.
View SolutionTwo parabola have the same focus. If their directrices are the x-axis and the y-axis respectively, then the slope of their common chord is :
View SolutionTwo parabolas have the same focus. If their directrices are the x- and the y-axis, respectively, then the slope of their common chord is ±1 (b) 43 (c) 34 (d) none of these
View Solution
