Two identical coils carry equal currents have a common centre and their planes are at right angles to each other. The ratio of the magnitude of the resulatant magnetic field at the centre and the field due to one coil is
The correct Answer is:C
To solve the problem, we need to find the ratio of the resultant magnetic field at the center of two identical coils that carry equal currents and are positioned at right angles to each other, compared to the magnetic field due to one coil.
1. Understanding the Setup:
- We have two identical coils with equal currents (I) and a common center.
- One coil lies in the xy-plane, while the other is perpendicular to it (let's say it lies in the xz-plane).
2. Magnetic Field Due to One Coil:
- The magnetic field (B) at the center of a single coil is given by the formula:
B1=μ0I2R
- Here, μ0 is the permeability of free space, I is the current, and R is the radius of the coil.
3. Direction of the Magnetic Field:
- For the coil in the xy-plane, the magnetic field direction (B1) is along the z-axis (k-cap).
- For the coil in the xz-plane, the magnetic field direction (B2) is along the y-axis (i-cap).
4. Magnetic Field Due to Both Coils:
- The magnetic field due to the first coil (B1) is:
B1=μ0I2R^k
- The magnetic field due to the second coil (B2) is:
B2=μ0I2R^i
5. Resultant Magnetic Field:
- The resultant magnetic field (B0) at the center is the vector sum of B1 and B2:
B0=B1+B2=μ0I2R^k+μ0I2R^i
- To find the magnitude of the resultant magnetic field:
|B0|=√B21+B22=√(μ0I2R)2+(μ0I2R)2
- This simplifies to:
|B0|=√2(μ0I2R)2=μ0I2R√2
6. Finding the Ratio:
- Now, we need to find the ratio of the resultant magnetic field (B0) to the magnetic field due to one coil (B1):
Ratio=|B0|B1=μ0I2R√2μ0I2R=√2
Final Answer:
The ratio of the magnitude of the resultant magnetic field at the center to the field due to one coil is:
√2:1
- We have two identical coils with equal currents (I) and a common center.
- One coil lies in the xy-plane, while the other is perpendicular to it (let's say it lies in the xz-plane).
- The magnetic field (B) at the center of a single coil is given by the formula:
B1=μ0I2R
- Here, μ0 is the permeability of free space, I is the current, and R is the radius of the coil.
- For the coil in the xy-plane, the magnetic field direction (B1) is along the z-axis (k-cap).
- For the coil in the xz-plane, the magnetic field direction (B2) is along the y-axis (i-cap).
- The magnetic field due to the first coil (B1) is:
B1=μ0I2R^k
- The magnetic field due to the second coil (B2) is:
B2=μ0I2R^i
- The resultant magnetic field (B0) at the center is the vector sum of B1 and B2:
B0=B1+B2=μ0I2R^k+μ0I2R^i
- To find the magnitude of the resultant magnetic field:
|B0|=√B21+B22=√(μ0I2R)2+(μ0I2R)2
- This simplifies to:
|B0|=√2(μ0I2R)2=μ0I2R√2
- Now, we need to find the ratio of the resultant magnetic field (B0) to the magnetic field due to one coil (B1):
Ratio=|B0|B1=μ0I2R√2μ0I2R=√2
The ratio of the magnitude of the resultant magnetic field at the center to the field due to one coil is:
√2:1
Topper's Solved these Questions
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Assertion and reason
20 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Match the following
4 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Check point
54 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Subjective
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
Similar Questions
The magnetic field at the centre of the current carrying coil is
View SolutionTwo identical coils have· a common centre and their planes are at right angles to each other and carry equal currents. If the magnitude of the induction field at the centre due to one of the coil is 'B ', then the resultant magnetic induction field due to combination at their common centre is
View SolutionTwo similar circular loops of radius R are lying concentrically with their planes at right angles to each other. The currents flowing in them are I and I√3 respectively. The magnetic field at the centre of the coil is
View SolutionTwo similar coils of radius R are lying concentriclaly with their planes at right angels to each other. The currents flowing in them are I and 2I respectively. The resulant magntic field induction at the centre will be
View SolutionTwo similar coils each of radius r and no. of turns n are lying concentrically with their planes at right angle to each other. The currents folowing in them are 1 A and √3A respectively. What is the magnetic field at centre of the coils ?
View SolutionA tightly wound 100 turn coil of radius 10cm is carrying a current of 1A. What is the magnitude of the magnetic field at the centre of the coil?
View SolutionThe magnitude of the magnetic field at O ( centre of the circular part ) due to the current - carrying coil as shown is :
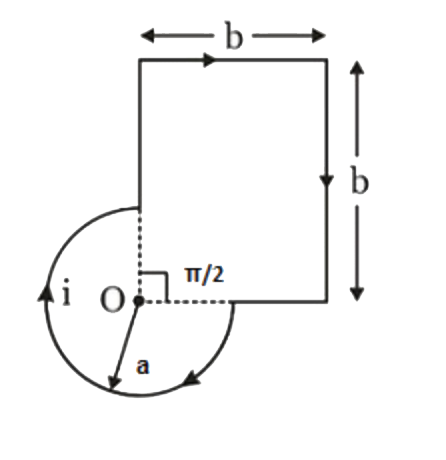
View SolutionTwo coils of wires A and B are mutually at right angles to each other as shown in the figure. If the current in one coil is changed, then in the other coil
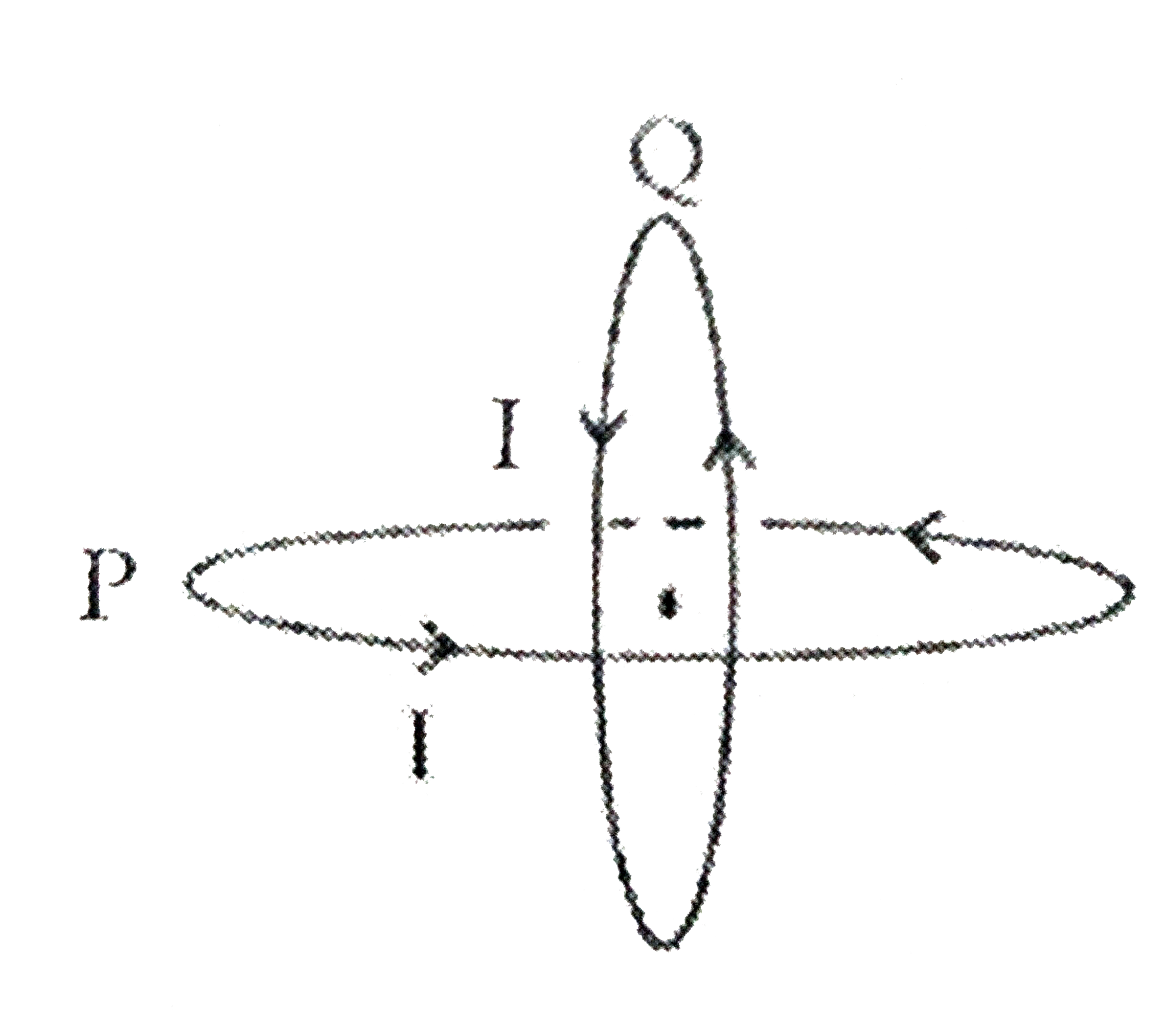
View SolutionTwo identical circular wires P and Q each of radius R and carrying current 'I' are kept in perpendicular planes such that they have a common centre as shown in the figure. Find the magnitude and direction of the net magnetic field at the common centre of the two coils.
View SolutionTwo circular coils of radii 5.0 cm and 10 cm carry equal currents of 2.0 A. The coils have 50 and 100 turns respectively and are placed in such a way that their planes are perpendicular to each other, what would be the magnitude of the magnetic field B at the centre ?
View Solution
