Tangents are drawn to the In -circle of triangle ABC which are prallel to its sides. If x,y,z be the lengths of the tangents and a,b,c be the sides of triangle, then prove that xa+yb+zc=1
Step by step video & image solution for Tangents are drawn to the In -circle of triangle ABC which are prallel to its sides. If x,y,z be the lengths of the tangents and a,b,c be the sides of triangle, then prove that x/a+y/b+z/c=1 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Tangent at P to the circumcircle of triangle PQR is drawn. If this tangent is parallel to side QR show that ΔPQR is isosceles.
View Solution(c) 103 (d) 10 18. A circle is inscribed in an equilateral triangle with side lengths 6 unit. Another circle is drawn inside the triangle (but outside the first circle), tangent to the first circle and two of the sides of the triangle. The radius of the smaller circle is (b) 2/3 (a) 1/ root3 (c) 2 (d) 1
View SolutionTangents are drawn from the point (-1, 2) to the parabola y2=4x The area of the triangle for tangents and their chord of contact is
View SolutionTangents are drawn from the point (-1, 2) to the parabola y2=4x The area of the triangle for tangents and their chord of contact is
View SolutionLet a,b,c be the sides of a triangle ABC, a=2c,cos(A-C)+cos B=1. then the value of C is
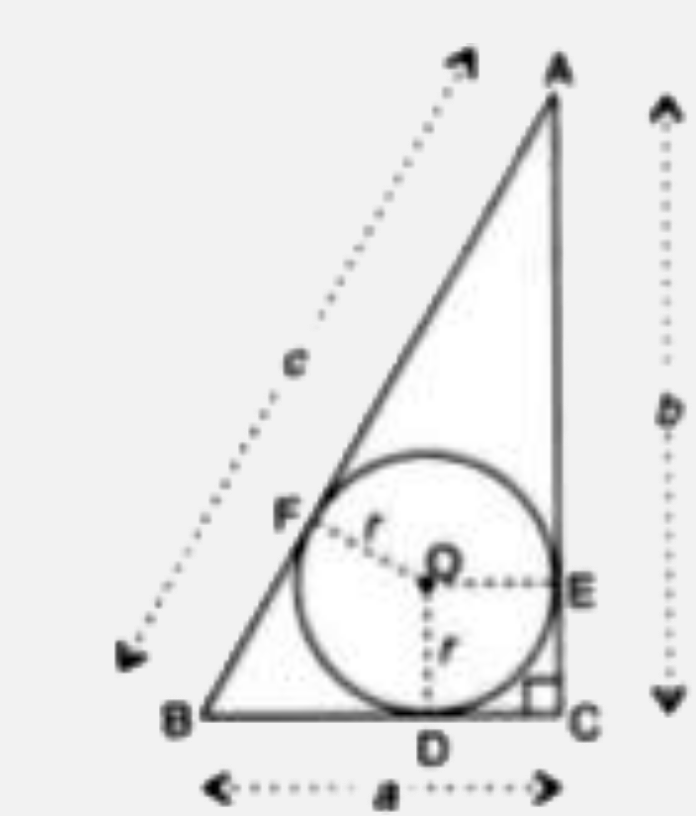
View SolutionIf a,b and c are sides of a ritht triangle where c is the hypotenuse, prove that the radius of the circle which touches the sides of the triangle is r=a+b−c2.
View SolutionIn a right triangle ABC, a circle with AB as diameter is drawn to intersect the hypotenuse AC in P. Prove that the tangent at P, bisects the side BC.
View SolutionA right angled isosceles triangle is inscribed in the circle x2+y2−4x−2y−4=0 then length of the side of the triangle is
View SolutionProve that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base. Given: A △ABC in which AB=AC and a circle is drawn by taking AB as diameter which intersects the side BC of triangle at D. To Prove: BD=DC Construction : Join AD.
View SolutionIf the plane x2+y3+z4=1 cuts the coordinate axes in A,B,C, then the area of triangle ABC is
View Solution
