If the anlges of elevation of the top of a tower from three collinear points A,B and C on a line leading to the foot of the tower are respectively , then the ratio AB:BC is
Step by step video solution for If the anlges of elevation of the top of a tower from three collinear points A,B and C on a line leading to the foot of the tower are 30^@ , 45^@ "and " 60 ^@ respectively , then the ratio AB:BC is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
If the angles of elevation of the top of a tower from three collinear points A, B and C, on a line leading to the foot of the tower, are 300 , 450 and 600 respectively, then the ratio, AB : BC, is : (1) √3:1 (2) √3:√2 (3) 1:√3 (4) 2:3
View SolutionThe angle of elevation of the top of a tower from a point 40 m away from its foot is 60∘. Find the height of the tower.
View SolutionThe angle of elevation of the top of a T.V. tower from three points A,B,C in a straight line in the horizontal plane through the foot of the tower are α,2α,3α respectively. If AB=a, the height of the tower is
View SolutionThe angle of elevation of the top of a tower from a point on the ground, which is 30m away from the foot of the tower is 30∘ . Find the height of the tower.
View SolutionThe angle of elevation of the top of a tower from a point on the ground, which is 30m away from the foot of the tower, is 30∘. Find the height of the tower.
View SolutionThe angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower is 30∘. Find the height of the tower.
View SolutionThe angle of elevation of the top of a tower from a point on the ground, which is 40 m away from the foot of the tower is 30∘. Find the height of the tower.
View SolutionThe angle elevation of the top of a tower from a point C on the ground. Which is 30 m away from the foot of the tower is 30∘ . Find the height of the tower.
 View Solution
View Solution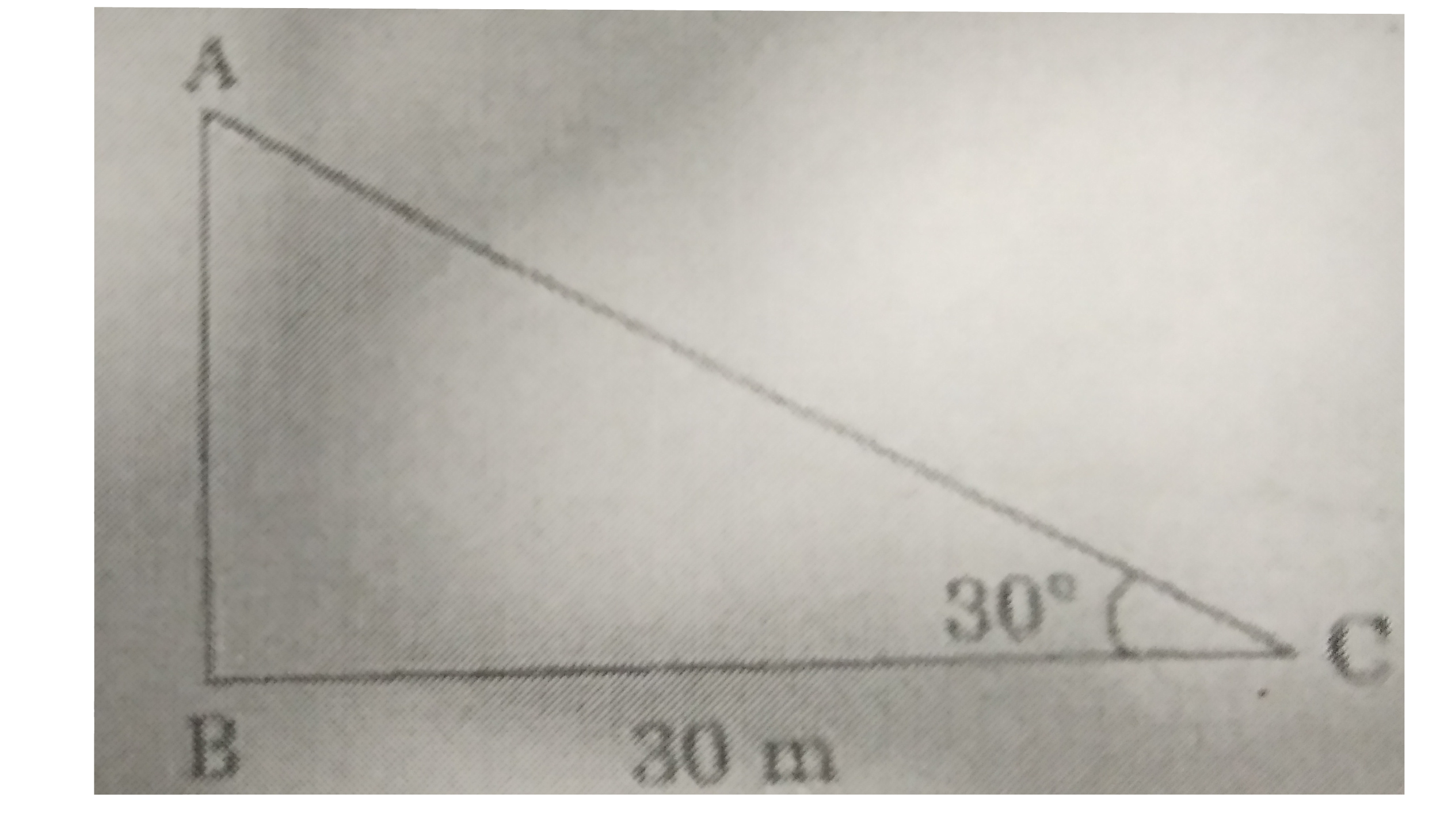
If figure, the angle of elevation of the top of a tower from a point C on the ground which is 30 m away from the foot of the tower, is 30∘. Find th height of the tower.View SolutionThe angle of elevation of the top of a tower from two distinct points s and t from foot are complementary. Prove that the height of the tower is √st.
View Solution

