Let ABC be an acute angled triangle whose orthocentre is at H. If altitude from A is produced to meet the circumcircle of triangle ABC at D , then prove HD=4RcosBcosCSolution in Tamil
OA=R
AH=2RcosA
2RcosA=R
cosA=12
A=60∘.
Topper's Solved these Questions
Similar Questions
If the lines joining the origin and the point of intersection of curves ax2+2hxy+by2+2gx+0 and a1x2+2h1xy+b1y2+2g1x=0 are mutually perpendicular, then prove that g(a1+b1)=g1(a+b).
View SolutionLet ABC be an acute angled triangle whose orthocentre is at H. If altitude from A is produced to meet the circumcircle of triangle ABC at D , then prove HD=4RcosBcosC
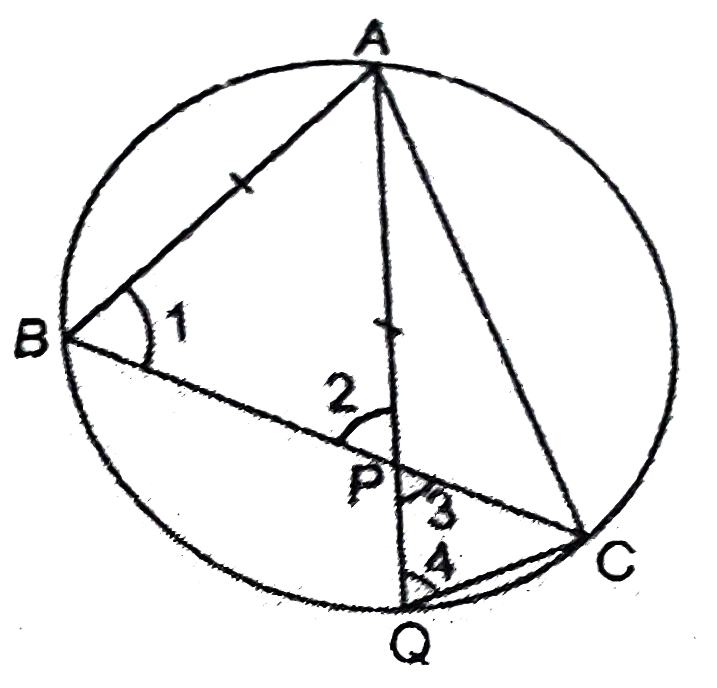
View SolutionIn given figure, ABC is a triangle produced meets the circumcircle of ΔABC at Q, prove that CP=CQ
View SolutionIf H is the orthocentre of ΔABC, then : cos(∠AHB)=
View SolutionIf H is the orthocentre of ΔABC, then AH=
View SolutionThe altitudes from the vertices A,B,C of an acute angled triangle ABC to the opposite sides meet the circumcircle at D,E,F respectively . Then EFBC=
View SolutionABC is an acute angled triangle with circumcenter O and orthocentre H. If AO=AH, then find the angle A.
View SolutionLet ABC be an acute angled triangle whose orthocentre is at H. If altitude from A is produced to meet the circumcircle of triangle ABC at D , then prove HD=4RcosBcosC
View SolutionABC is an acute angled triangle with circumcenter O and orthocentre H. If AO=AH, then find the angle A.
View SolutionABC is an acute angled triangle with circumcenter O and orthocentre H. If AO=AH, then find the angle A.
View SolutionIf H is the orthocentre of a acute-angled triangle ABC whose circumcircle is x2+y2=16 then circum diameter of the triangle HBC is
View SolutionIf AD, BE, CF are the altitudes of ΔABC whose orthocentre is H, then C is the orthocentre of :
View SolutionIn the given I is the incentre of triangle ABC. AI produced meets the circumcircle of triangle ABC at point D. Given that angle ABC=48∘and angle ACB=72∘, calculate:
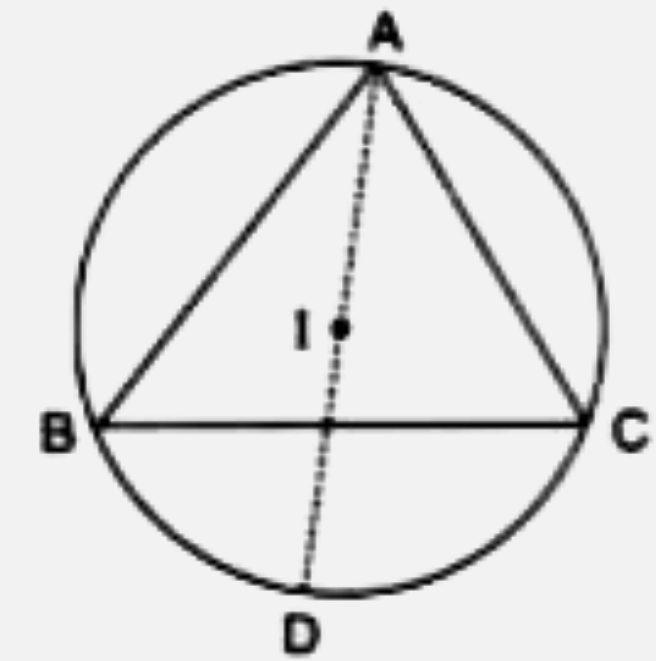
∠CBD
View SolutionIn the given I is the incentre of triangle ABC. AI produced meets the circumcircle of triangle ABC at point D. Given that angle ABC=48∘and angle ABC=72∘, calculate:
∠DCI
View SolutionIn the given I is the incentre of triangle ABC. AI produced meets the circumcircle of triangle ABC at point D. Given that angle ABC=48∘and angle ABC=72∘, calculate:
∠BIC
View SolutionIn given figure , ABC is a triangle produced meets the circumcircle of ΔABC at Q, prove that CP=CQ
View Solution