The number of roots of the equation is 2 (b) 3 (c) 4 (d) 0Solution in Tamil
We have x sin x = 1
Number of roots of the above equation = number of points (s) of the intersection of the graphs of and for
The graphs of both functions are as shown in the following figure.
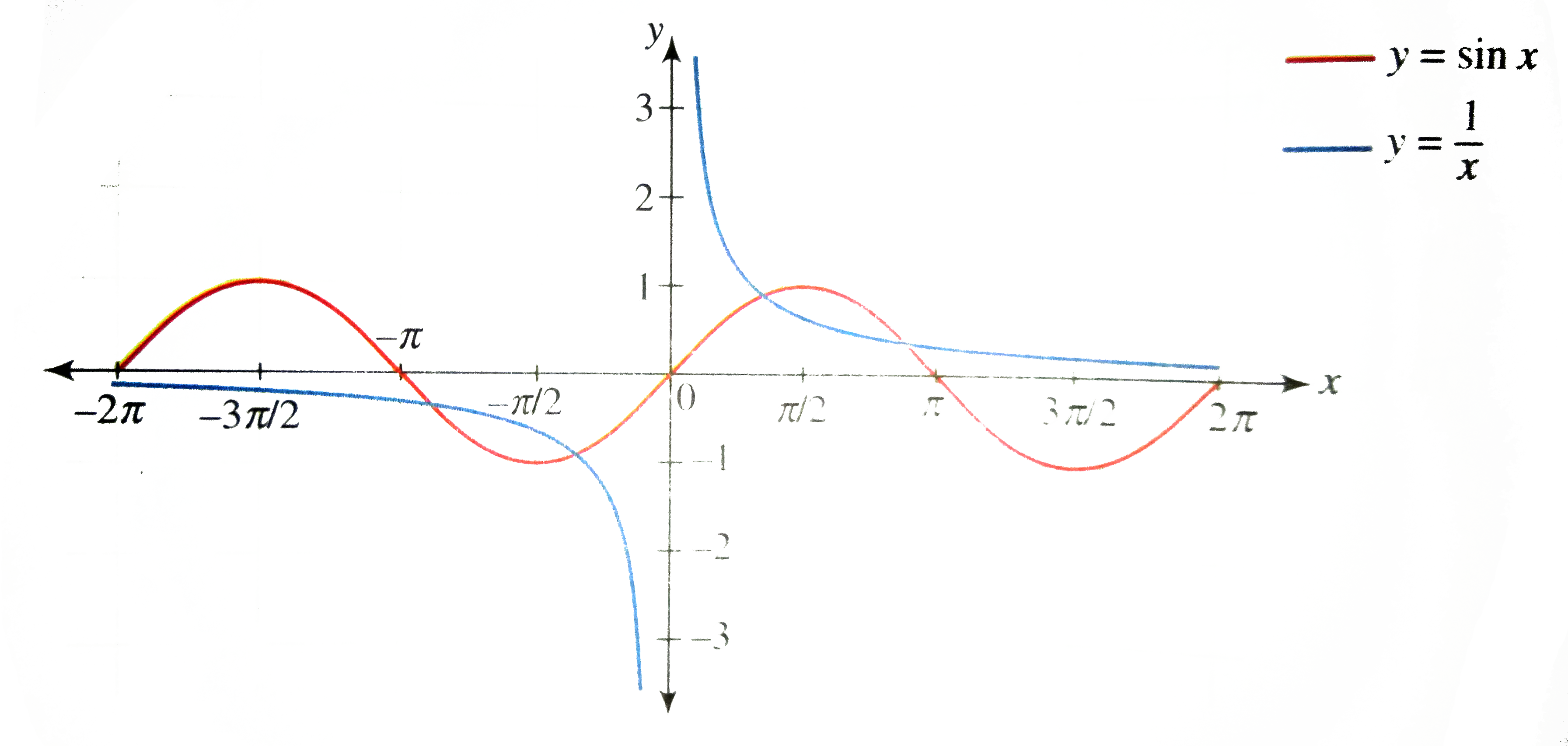
Graphs intersect at four points, hence four roots.
Similar Questions
Find the number of roots of the equation xsinx=1,x∈[−2π,0)∪(0,2π].
View SolutionIf |cotx+cosecx|=|cotx|+|cosecx|,x∈[0,2π], then complete set of values of x is : (a).[0,π] (b).(0,π2] (c).(0,π2]∪[3π2,2π) (d).(π,3π2]∪[7π4,2π]
View SolutionThe number of real roots of the equation |x|^(2) - 3|x| + 2 = 0 is a)1 b)2 c)3 d)4
View SolutionNumber of roots of equation 3|x|−|2−|x∣∣=1 is a. 0 b. 2 c. 4 d. 7
View SolutionThe number of solution of equation 2cos−1x=a+a2(cos−1x)−1 are at least (a) 1 if a∈[−2π,π]−{0} (b) 1 if a ∈(0,π] (c) 1 if a∈[−2π,0) (d) 2 if a>0
View SolutionNumber of roots of equation 3|x|−|2−|x∣∣=1 is a. 0 b. 2 c. 4 d. 7
View SolutionThe number of real roots of the equation x2tanx=1 lies between 0and2π is/are
(A) 1 (B) 2 (C) 3 (D) 4
View SolutionLet f(x)=max{tanx,cotx}. Then number of roots of the equation f(x)=1√3∈(0,2π) is (A) 2 (B) 4 (C) 0 (D) infinite
View Solution
