At the endpoint and midpoint of a circular are AB, tangent lines are drawn, and the points, A and B are jointed with a chord. Prove that the ratio of the areas of the triangles thus formed tends to 4 as the arc AB decreases infinitely.Solution in Tamil
Step by step video & image solution for At the endpoint and midpoint of a circular are AB, tangent lines are drawn, and the points, A and B are jointed with a chord. Prove that the ratio of the areas of the triangles thus formed tends to 4 as the arc AB decreases infinitely. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
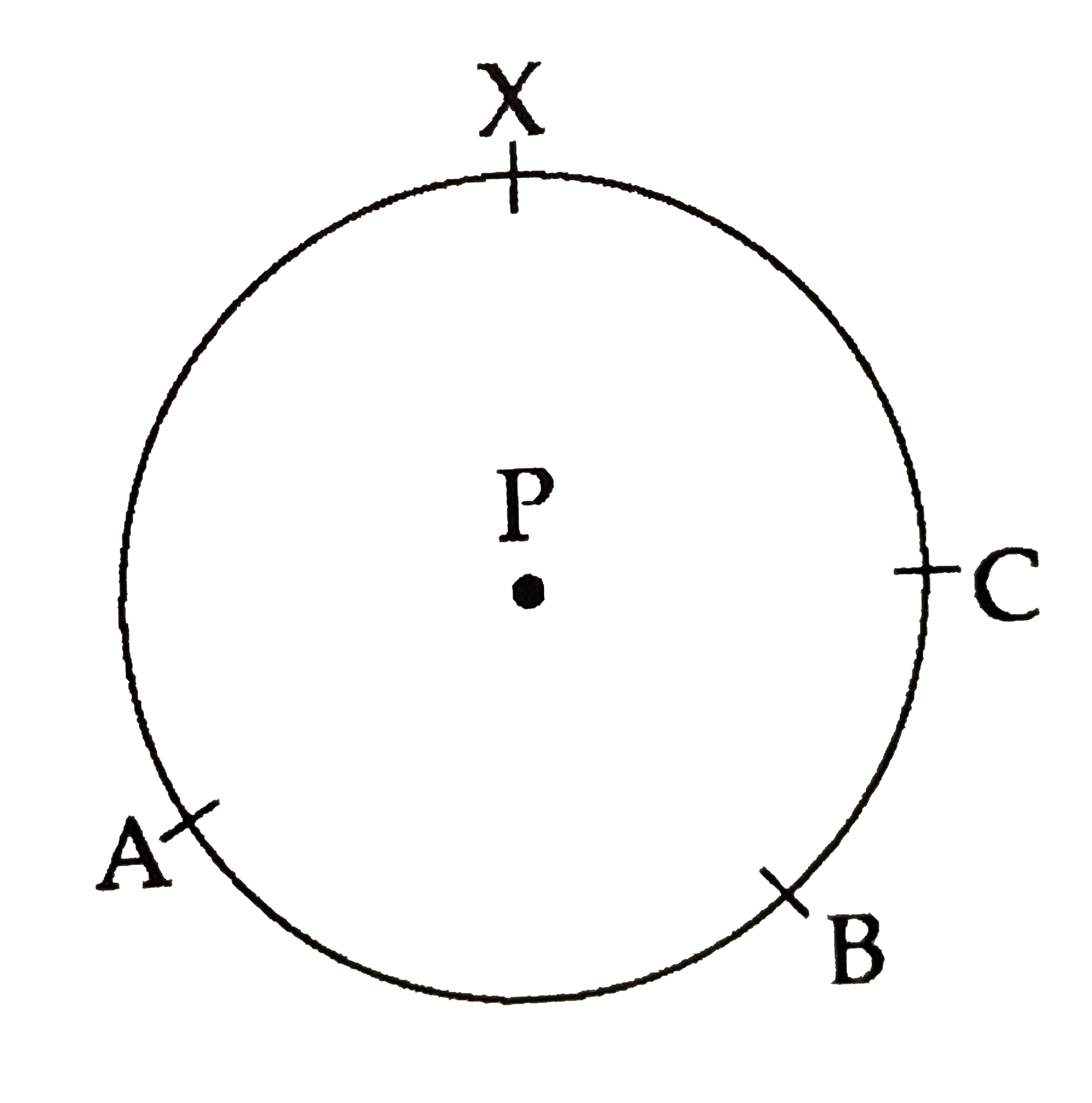
A circle with centre P. arc AB = arc BC and arc AXC = 2 arc AB . Find measure of arc AB, arc BC and arc AXC. Prove that chord AB≅ chord BC .
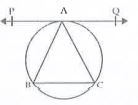
View SolutionLine PQ is a tangent to the circle at point AB ≅ arc AC. Complete the following activity to prove ΔABC as isosceles triangle.
View SolutionFrom the point (4, 6) a pair of tangent lines are drawn to the parabola, y2=8x. The area of the triangle formed by these pair of tangent lines & the chord of contact of the point (4, 6) is
View SolutionFrom a point A(3,2) , tangents are drawn to the circle x2+y2−2x+4y−4=0 . If BC is the chord of contact of tangents , show that the line joining the midpoints of AB and AC is 4x+8y-17=0
View Solution. Prove that the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc.
View SolutionAt the endpoint and midpoint of a circular are AB, tangent lines are drawn, and the points, A and B are jointed with a chord. Prove that the ratio of the areas of the triangles thus formed tends to 4 as the arc AB decreases infinitely.
View Solutionदो वृत्त परस्पर P बिंदु पर बाह्यतः स्पर्श करते हैं और उभयनिष्ठ स्पर्श रेखाएं उन्हें A और B पर स्पर्श करती हैं तो सिद्ध कीजिए (i) P से खींची गई उभयनिष्ठ स्पर्श रेखाएं AB को समद्विभाजित करती है|
(ii) रेखा AB बिंदु P पर समकोण अंतरित करती है।
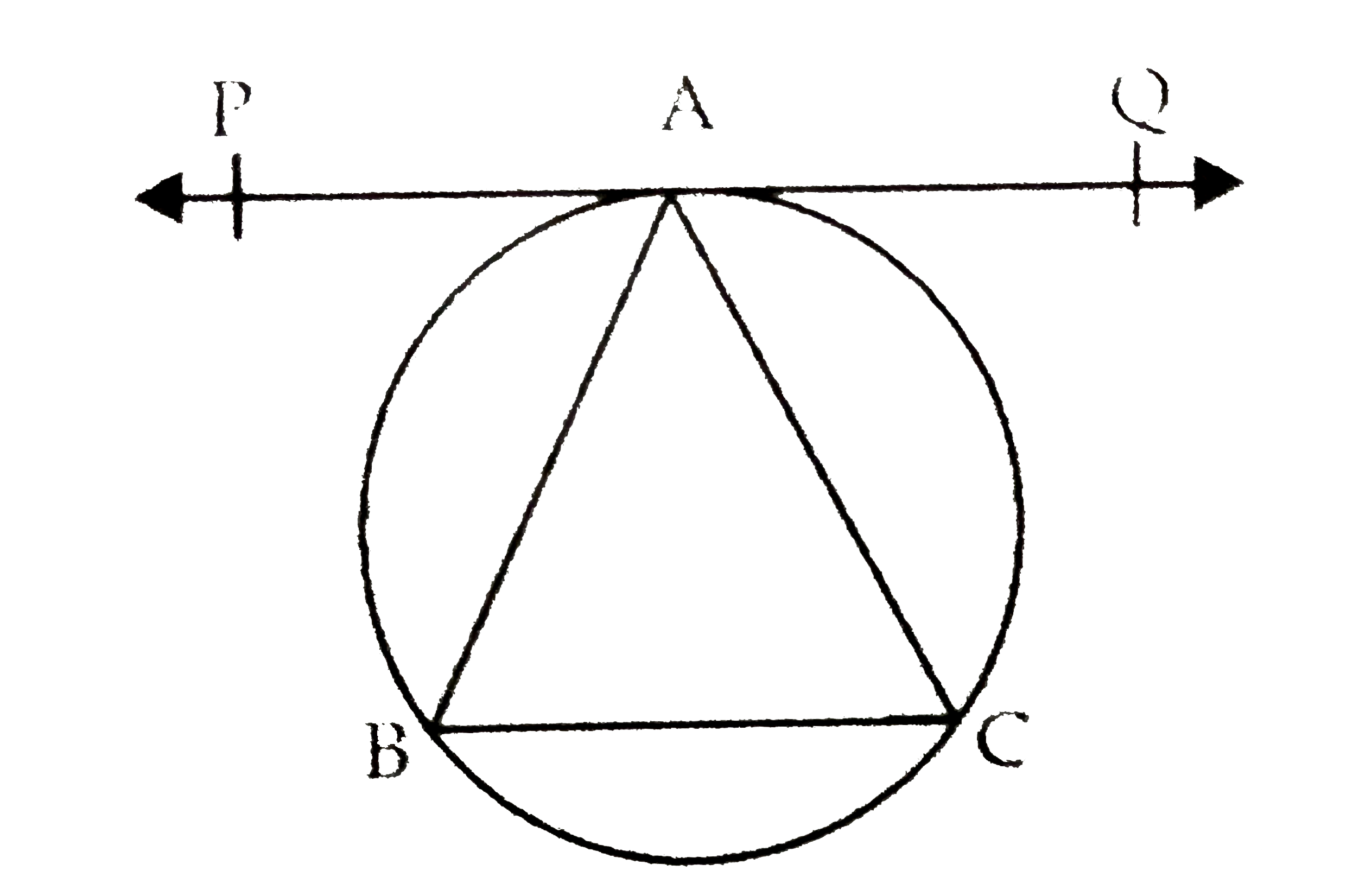
View SolutionLine PQ is a tangent to the circle at point A, arcAB≅arcAC. Prove that △ABC is isosceles triangle.
View Solution
