The maximum value of ∣∣∣arg(11−z)∣∣∣ for |z|=1,z≠1 is given by.Solution in Tamil
Step by step video & image solution for The maximum value of |a r g(1/(1-z))| for |z|=1,z!=1 is given by. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Similar Questions
For |z−1|=1, show that tan{arg(z−1)2}−(2iz)=−i
04:17View SolutionGiven that 1+2|z|2=∣∣z2+1∣∣2+2|z+1|2, then the value of |z(z+1)| is ______.
06:14View SolutionFind the maximum and minimum values of |z| satisfying ∣∣∣z+1z∣∣∣=2
03:04View SolutionIf z2+z+1=0 then 6∑r=1(zr+1zr)2=
06:15View SolutionIf the complex number z is such that |z−1|≤1and|z−2|=1 find the maximum possible value |z|2
05:28View SolutionThe shaded region, where P=(−1,0),Q=(−1+√2,√2)R=(−1+√2,−√2),S=(1,0) is represented by Figure
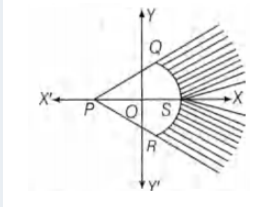
|z+1|>2,∣arg(z+1)<π4
|z+1|<2,∣arg(z+1)<π2
|z+1|>2,∣arg(z+1)>π4
|z+1|<2,∣arg(z+1)>π203:40View SolutionFor |z−1|=1, show that tan{arg(z−1)2}−(2iz)=−i
05:33View SolutionFor |z-1|=1, show that tan{[a r g(z-1)]/2}-((2i)/z)=-i
04:20View Solution

