If z is a complex number such that −π/2≤argz≤π/2, then which of the following inequality is true? (a)|z−z|≤|z|(argz−argz) b. |z−z|≥|z|(argz−argz) c.|z−z|<(argz−argz) d. none of theseSolution in Tamil
Step by step video & image solution for If z is a complex number such that -pi//2lt=a r g zlt=pi//2, then which of the following inequality is true? (a)|z- z |lt=|z|(a r g z-a r g z ) b. |z- z |geq|z|(a r g z-a r g z ) c.|z- z |<(a r g z-a r g z ) d. none of these by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Similar Questions
The shaded region, where P=(−1,0),Q=(−1+√2,√2)R=(−1+√2,−√2),S=(1,0) is represented by Figure
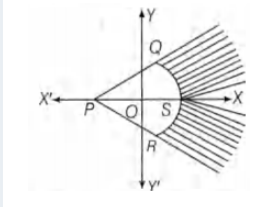
|z+1|>2,∣arg(z+1)<π4
|z+1|<2,∣arg(z+1)<π2
|z+1|>2,∣arg(z+1)>π4
|z+1|<2,∣arg(z+1)>π203:40View SolutionIf arg(z)<0, then arg(−z)−a r g(z) equals π (b) −π (d) −π2 (d) π2
03:56View SolutionIf |z−2−i|=|z|sin(π4−argz)∣∣∣ , where i=√−1 ,then locus of z, is
04:04View SolutionIf arg[z1(z3−z2)]=a r g[z3(z2−z1)] , then find prove that O,z1,z2,z3 are concyclic, where O is the origin.
04:25View SolutionIf arg(z)<0, then arg(−z)−arg(z) equals π (b) −π (d) −π2 (d) π2
02:47View SolutionIf z is a complex number such that -pi//2lt=a r g zlt=pi//2, then which of the following inequality is true? a. |z- z |lt=|z|(a r g z-a r g z ) b. |z- z |geq|z|(a r g z-a r g z ) c. |z- z | d. none of these
03:17View SolutionIf arg[z1(z3−z2)]=arg[z3(z2−z1)] , then prove that O,z1,z2,z3 are concyclic, where O is the origin.
03:01View Solution

