Consider a curve C:y=cos−1(2x−1) and a straight line L:2px−4y+2π−p=0. Statement 1: The set of values of p for which the line L intersects the curve at three distinct points is [−2π,−4]. Statement 2: The line L is always passing through point of inflection of the curve C.Solution in Tamil
Step by step video & image solution for Consider a curve C : y=cos^(-1)(2x-1) and a straight line L :2p x-4y+2pi-p=0. Statement 1: The set of values of p for which the line L intersects the curve at three distinct points is [-2pi,-4]dot Statement 2: The line L is always passing through point of inflection of the curve Cdot by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
माना बिंदु P(2,−1) तथा x−y+1=0 सरल रेखा l है। यदि बिंदु P का रेखा l के सापेक्ष प्रतिबिम्ब Q हो, तो Q का y-अक्ष के सापेक्ष प्रतिबिम्ब है-
View SolutionLet C:x2+y2=9,E:x29+y24=1 and L : y = 2x be three curves. IF R is the point of intersection of the line L with the line x =1 , then
View SolutionA line L passing through the focus of the parabola (y−2)2=4(x+1) intersects the two distinct point. If m be the slope of the line I,, then
View SolutionThe point C is the image of point A in line l and line segment BC intersects the line l at P.
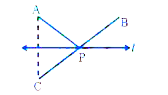
Is the image of P in line l the point P itself ?
View SolutionConsider a curve C:y=cos−1(2x−1) and a straight line L:2px−4y+2π−p=0. Statement 1: The set of values of p for which the line L intersects the curve at three distinct points is [−2π,−4]. Statement 2: The line L is always passing through point of inflection of the curve C.
View SolutionA line L passing through the focus of the parabola y2=4(x−1) intersects the parabola at two distinct points. If m is the slope of the line L,then
View SolutionConsider a curve ax2+2hxy+by2=1 and a point P not on the curve. A line drawn from the point P intersect the curve at points Q and R. If the product PQ.PR is independent of the slope of the line, then show that curve is a circle.
View Solution
