Consider a curve C:y=cos−1(2x−1) and a straight line L:2px−4y+2π−p=0. Statement 1: The set of values of p for which the line L intersects the curve at three distinct points is [−2π,−4]. Statement 2: The line L is always passing through point of inflection of the curve C.Solution in Bengali
Step by step video & image solution for Consider a curve C : y=cos^(-1)(2x-1) and a straight line L :2p x-4y+2pi-p=0. Statement 1: The set of values of p for which the line L intersects the curve at three distinct points is [-2pi,-4]dot Statement 2: The line L is always passing through point of inflection of the curve Cdot by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Given two points A and B. If area of triangle ABC is constant then locus of point C in space is
View SolutionFind the area of the figure enclosed by the curve 5x2+6xy+2y2+7x+6y+6=0.
View SolutionConsider a curve ax^(2)+2hxy+by^(2)-1=0 and a point P not on the curve.A line is drawn from the point P intersects the curve at the point Q and R.If the product PQ.PR is independent of the s[ope of the line,then the curve is:
View SolutionA line L is perpendicular to the curve y=(x^(2))/(4)-2 at its point p and passes through (0,-1). The coordinates of the point p are
View SolutionFind the set of values of p for which line 2px−4y+2π−9=0 intersect the curve y=cos−1at three distinct points.
View SolutionLet C:x2+y2=9,E:x29+x24=1 and L : y = 2x be three curves. IF R is the point of intersection of the line L with the line x =1 , then
View SolutionConsider the curve y=x2 and the straight line y=2x+3.
(i) Find the points of intersection of the given curve and the straight line.
(ii) Find the area of the region bounded by the given curve and the straight line.
View SolutionConsider a curve C:y=cos−1(2x−1) and a straight line L:2px−4y+2π−p=0. Statement 1: The set of values of p for which the line L intersects the curve at three distinct points is [−2π,−4]. Statement 2: The line L is always passing through point of inflection of the curve C.
View SolutionA line L passing through the focus of the parabola y2=4(x−1) intersects the parabola at two distinct points. If m is the slope of the line L, then (a) −1<m<1 (b) m<−1 or m>1 (c) m∈R (d) none of these
View SolutionA line L passes through the point (1, 1) and (2,0). Another line M which is perpendicular to L passes through the point [12,0]. Then the area of the triangle formed by the lines L, M and y-axis is
View Solutionमाना बिंदु P(2,−1) तथा x−y+1=0 सरल रेखा l है। यदि बिंदु P का रेखा l के सापेक्ष प्रतिबिम्ब Q हो, तो Q का y-अक्ष के सापेक्ष प्रतिबिम्ब है-
View SolutionLet C:x2+y2=9,E:x29+y24=1 and L : y = 2x be three curves. IF R is the point of intersection of the line L with the line x =1 , then
View SolutionA line L passing through the focus of the parabola (y−2)2=4(x+1) intersects the two distinct point. If m be the slope of the line I,, then
View SolutionConsider a curve C : y=cos^(-1)(2x-1) and a straight line L :2p x-4y+2pi-p=0. Statement 1: The set of values of p for which the line L intersects the curve at three distinct points is [-2pi,-4]dot Statement 2: The line L is always passing through point of inflection of the curve Cdot
View SolutionThe point C is the image of point A in line l and line segment BC intersects the line l at P.
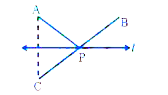
Is the image of P in line l the point P itself ?
View Solution
