If the sum of the distances of a point from two perpendicular lines in a plane is 1, then its locus is a (a) square (b) a circle (c) a straight line (d) two intersecting linesSolution in Tamil
a square
a circle
a straight line
two intersecting lines
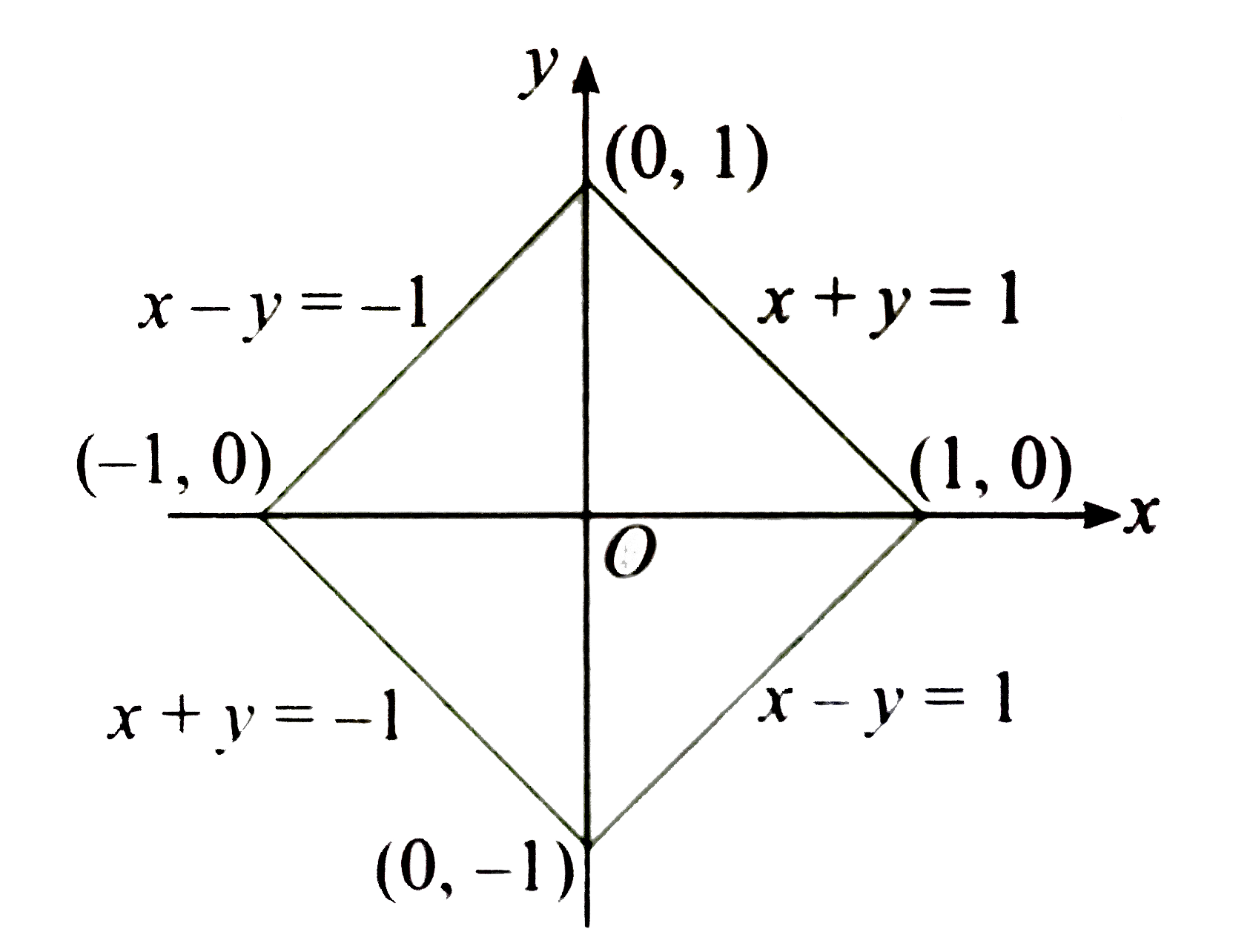
Let the two perpendicular lines be taken as the coordinates axes. If (h,k) is any point on the locus, then according to the given condition, |h|+|k|=1. Hence, the locus of (h,k) is |x|+|y|=1. This consists of four line segments enclosing a square as shown in the figure.
Similar Questions
A point moves so that the sum of the squares of its distances from two intersecting straight lines is constant. Prove that its locus is an ellipse.
04:37View Solutionदो परस्पर लम्बवत् सरल रेखाओं पर स्थित एक बिन्दु P से दूरी का योग 1 इकाई है, तब P का बिन्दुपथ है
05:07View SolutionAssertion (A): The sum of the distances of a point from two perpendicular lines is 1, then its locus is a square
Reason (R): The locus of a point which is at a distance 'p' from the given point is a circle06:04View SolutionIf p1,p2 are the perpendicular distance from the origin to the two straight lines which are perpendicular to each other, then the locus of the point of intersection of the perpendicular lines is
05:18View SolutionIf the sum of the distances of a point from two perpendicular lines in the plane is 1, then its locus is
03:47View SolutionA point moves such that the sum of the square of its distances from two fixed straight lines intersecting at angle 2alpha is a constant. Prove that the locus of points is an ellipse
06:17View SolutionIf the sum of the distances of a point from two perpendicular lines in a plane is 1, then its locus is (a)a square (b) a circle (c) a straight line (d) two intersecting lines
04:24View Solution

