Point M moves on the circle (x−4)2+(y−8)2=20. Then it brokes away from it and moving along a tangent to the circle, cuts the x-axis at the point (-2,0). The co-ordinates of a point on the circle at which the moving point broke away is Solution in Tamil
Step by step video & image solution for Point M moves on the circle (x-4)^2+(y-8)^2=20. Then it brokes away from it and moving along a tangent to the circle, cuts the x-axis at the point (-2,0). The co-ordinates of a point on the circle at which the moving point broke away is by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
बिन्दु A(-1, 1) व वृत्त x2+y2=4 पर एक गतिशील बिन्दु P को मिलाने वाली रेखा को 3 : 2 में विभाजित करने वाले बिन्दु का बिन्दुपथ होगा
View SolutionOn a circle of radius 4 cm, draw a tangent line from the point, which is 6 cm away from the center of this circle.
View Solutionबिंदु M वृत्त (x−4)2+(y−8)2=20 पर घूम रहा है। ये वृत्त से अलग होता है तथा वृत्त की स्पर्श रेखा के अनुदिश जाते हुए x - अक्ष को बिंदु (-2,0) पर काटता है। वृत्त पर उस बिंदु के निर्देशांक जहाँ घूमता बिंदु वृत्त से अलग होता है , है -
View Solutionबिन्दु M वृत्त (x−4)2+(y−8)2=20 पर घूम रहा है | ये वृत्त से अलग होता है तथा वृत्त की स्पर्श रेखा के अनुदिश जाते हुए x-अक्ष को बिन्दु (-2, 0) पर काटता है | वृत्त पर उस बिन्दु के निर्देशांक जहाँ घूमता बिन्दु वृत्त से अलग होता है है
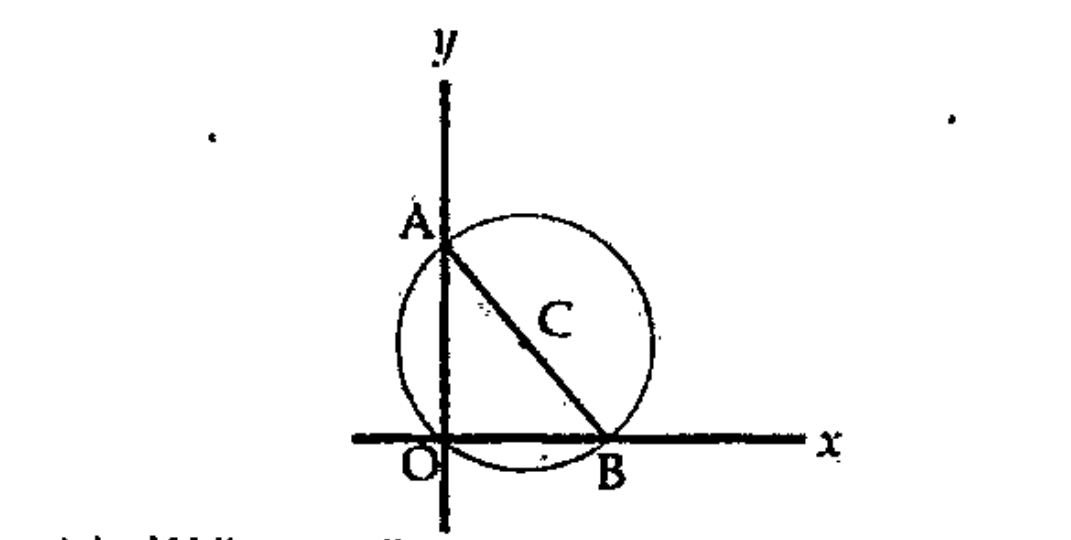
View SolutionC is the centre of the circle passing through the origin. Circle cuts the y-axis at A(0,4) and the x-axis at B(4,0).(0,0) is the point on the circle. There is one more point on the circle with x and y coordinates equal. Which is that point?
 .
.
View SolutionFind the equation of the Circle whose centre is at the point (4, 5) and which touches the x-axis. Also find the co-ordinates of the points at which the circle cuts the y-axis.
View SolutionPoint M moved on the circle (x−4)2+(y−8)2=20 Then it broke away from it and moving along a tangent to the circle, cuts the x-axis at the point(-2, 0) The co-ordinates of a point on the circle at which the moving point broke away is
View SolutionA chord of the circle x2+y2=a2 cuts it at two points A and B such that ∠AOB=π/2, where O is the centre of the circle. If there is a moving point P on this circle, then the locus of the orthocentre of ΔPAB will be a
View Solution
