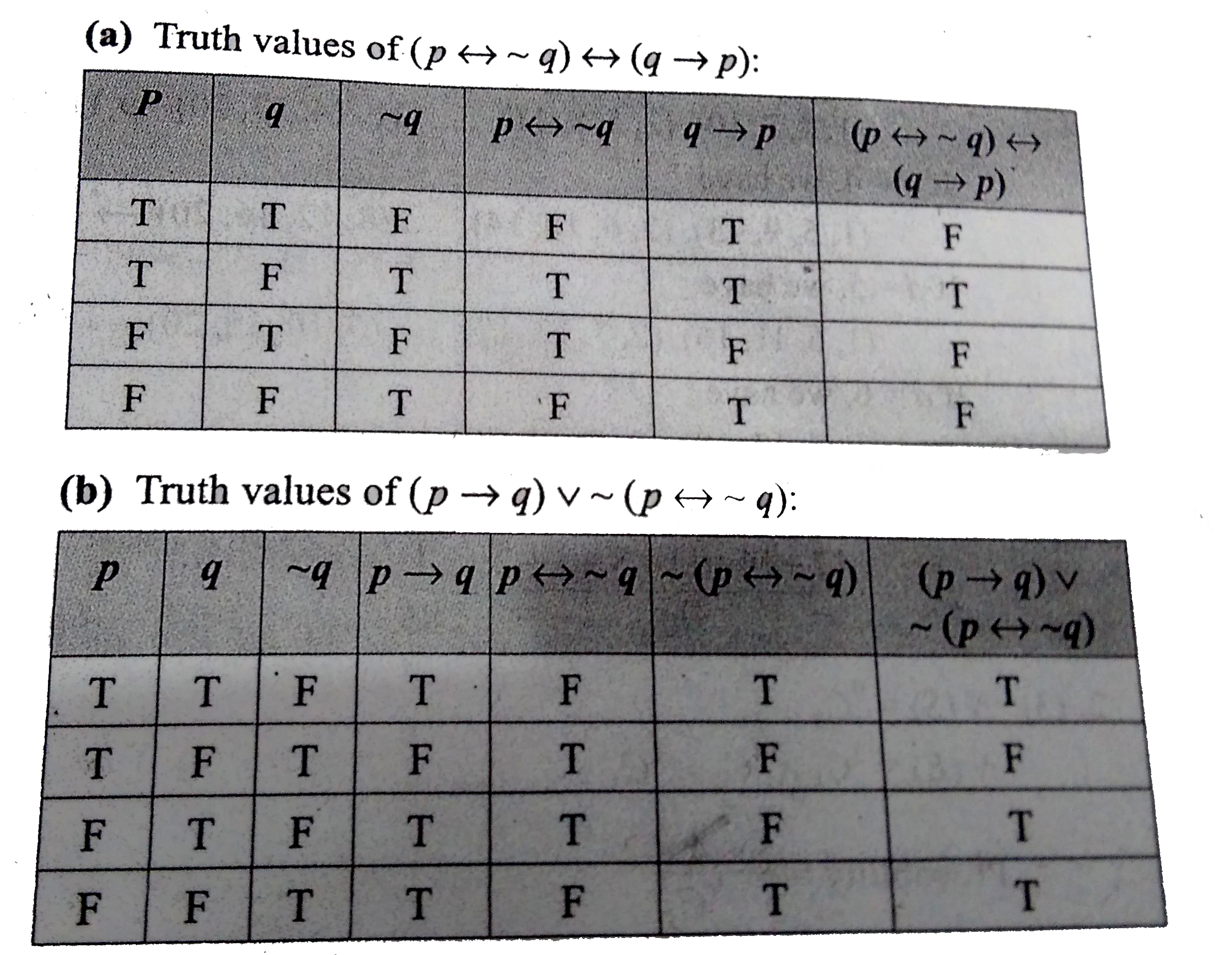
Find the truth values of
(a)(p↔~q)↔(p→p) (b)(p→q)∨~(p↔~q) Solution in Tamil
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - MATHMETICAL REASONINGEXERCISE - Exercise 10.25videos
MATHMETICAL REASONING
- BOOK - CENGAGECHAPTER - MATHMETICAL REASONINGEXERCISE - Exercise (Single)38videos
MATHMETICAL REASONING
- BOOK - CENGAGECHAPTER - MATHMETICAL REASONINGEXERCISE - JEE Previous Year10videos
MATHMETICAL REASONING
- BOOK - CENGAGECHAPTER - LOGARITHM AND ITS PROPERTIESEXERCISE - JEE Previous Year5videos
LOGARITHM AND ITS PROPERTIES
- BOOK - CENGAGECHAPTER - MATRICESEXERCISE - Multiple Correct Answer7videos
MATRICES
Similar Questions
Show that (p∧q)∨(~p)∨(p∧~q) is a tautology
05:26View SolutionWhich of the following is not a statement.
03:36View SolutionStatement-1: ~(p↔~q) is equivalent to (p↔q).
Statement-2: ~(p↔~q) is a tautology.01:59View SolutionShow that the equation esinx−e−sinx−4=0 has no real solution.
03:49View SolutionIf A=⎡⎢⎣100101010⎤⎥⎦, then
03:10View SolutionFind the truth values of
(a)(p↔~q)↔(p→p) (b)(p→q)∨~(p↔~q)01:40View SolutionShow that ~(p↔q)≡(p∧~q)∨(~p∧q).
03:43View SolutionIf p and q have truth value 'F', then the truth values of (~p∨q)↔~(p∧q) and p↔(p→~q) are respectively
05:43View SolutionIf p is true and q is false then the truth values of (p↔q)↔(~q→~p) and (~p∨q)∧(~q∨p) are respectively
03:25View Solution~(p⇒q)⇔~p∨~q is-
02:43View SolutionThe compound statement (p⇔q)∨(p⇔~q) is logically equivalent to
03:18View Solution~ (p rArr q) hArr ~ p vv ~ q is
02:50View SolutionFind the truth values of
(a)(p↔~q)↔(p→p) (b)(p→q)∨~(p↔~q)02:11View SolutionShow that ~(p↔q)≡(p∧~q)∨(~p∧q).
04:05View SolutionIf p and q have truth value 'F', then the truth values of (~p∨q)↔~(p∧q) and p↔(p→~q) are respectively
11:10View Solution