Consider the function f(x)={x−[x]−12,ifx∉Io,ifx∈I,where[.] denotes the fractional integral function and I is the set of integers. Then find g(x)=max.x2,f(x),|x|;−2≤x≤2.Solution in Tamil
We first draw the graphs of y=f(x),y=x2andy=|x|y=f(x),y=x2andy=|x|.
To deaw the graph of y=x−[x]−0.5={x}−0.5, we shift the graph of y={x},0.5 units downward vertically for non-nitegral values of x and plotting '0' for integral values fo x as shown in the following in the following figure.
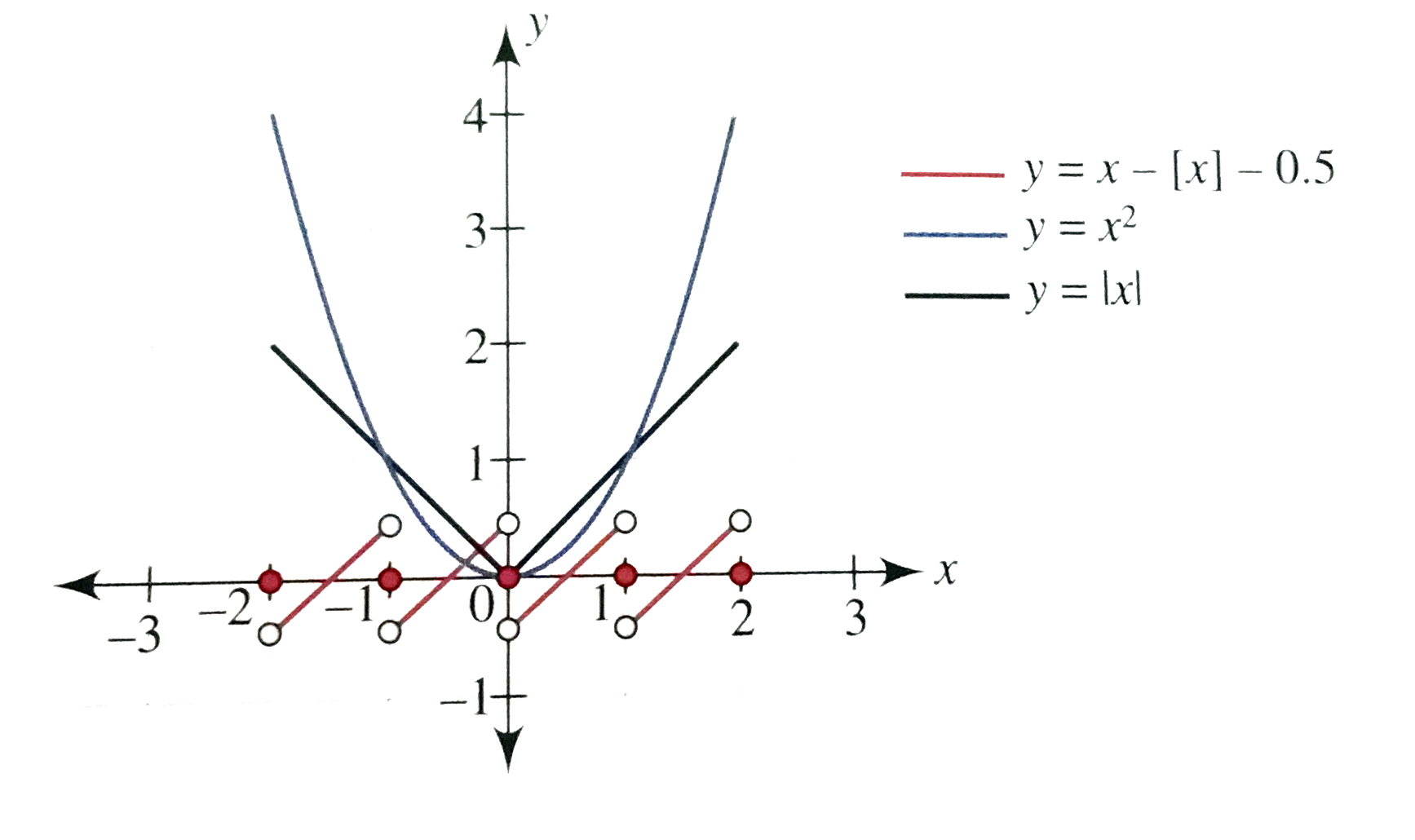
Clearly, from the graph, g(.x) =⎧⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪⎩x2,−2≤x≤−11−x,−1≤x≤−1/412+x,−14<x<01+x,0≤x≤1x2,1≤≤2
Topper's Solved these Questions
- GRAPHICAL TRANSFORMATIONSBOOK - CENGAGECHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise
14 Videos
- GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
18 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises
4 Videos
Similar Questions
Draw the graph of y=tan−1x−cot−1x.
View SolutionDraw the graph of y=tan−1x+cot−1x
View SolutionSketch the graph of an example of a rational function f that satisfies all the given conditions.
(i) f(0)=0,f(1),limx→∞f(x)=0,f is odd
(ii) limx→0+f(x)=∞,limx→0−f(x)=−∞,limx→∞f(x)=1,limx→−∞f(x)=1
(iii) limx→−2f(x)=∞,limx→−∞f(x)=3,limx→∞f(x)=3,f(0)=0
View SolutionLet A={x∈R:0≤x≤1}. If f:A→A is defined by f(x)={x,ifxQ1−x,ifxQ then prove that fof(x)=x for all x∈A.
View SolutionIf f(x0=x+{−x}+[x], where [x] is the integral part& {x} is the fractional part of x. Discuss the continuity of f in [−2, 2] .
View SolutionConsider the function f(x)={x−[x]−12x∉0x∈I where [.] denotes the fractional integral function and I is the set of integers. Then find g(x)max.[x2,f(x),|x|},−2≤x≤2.
View SolutionFind the points of discontinuity of the function: f(x)=[[x]]−[x−1],where[.] represents the greatest integer function
View SolutionDiscuss the differentiability of f(x)=[x]+|1−x|,x∈(−1,3),where[.] represents greatest integer function.
View Solution∫x02t2[t]dt,where[.] denotes the greatest integer function and x∈R+ , is equal to
View SolutionConsider the function f(x)={x−[x]−12x∉0x∈I where [.] denotes the fractional integral function and I is the set of integers. Then find g(x)max.[x2,f(x),|x|},−2≤x≤2.
View SolutionDiscuss the differentiability of f(x)=[x]+|1−x|,x∈(−1,3),where[.] represents greatest integer function.
View SolutionDiscuss the continuity of the function f(x)={2x−1,ifx<2,3x2,ifx≥2at x=2
View SolutionLet A={x∈R:0≤x≤1}. If f:A→A is defined by f(x)={x,ifx∈Q,1−x,ifx∉Q then prove that fof(x)=x for all x∈A.
View SolutionFind the points of discontinuity of the function: f(x)=[[x]]−[x−1],where[.] represents the greatest integer function
View SolutionDiscuss the differentiability of f(x)=[x]+|1−x|,x∈(−1,3),where[.] represents greatest integer function.
View SolutionConsider the function f(x)={x−[x]−12x∉0x∈I where [.] denotes the fractional integral function and I is the set of integers. Then find g(x)max.[x2,f(x),|x|},−2≤x≤2.
View Solution
