The reflection of the point $\to a$ in the plane $\to r . \to n = q$ is (A) $\to a + \frac{\to q - \to a . \to n}{| \to n |}$ (B) $\to a + 2 (\frac{\to q - \to a . \to n}{{| \to n |}^{2}}) \to n$ (C) $\to a + \frac{2 (\to q + \to a . \to n)}{| \to n |}$ (D) none of theseSolution in Tamil

A

$\to a + \frac{(\to q - \to a . \to n)}{| \to n |}$

B

$\to a + 2 (\frac{(\to q - \to a . \to n)}{{| \to n |}^{2}}) \to n$

C

$\to a + \frac{2 (\to q - \to a . \to n)}{| \to n |} \to n$

D

none of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:b

Given plane is $\to r . \to n = q$
Let the image of $A (\to a)$ in the plane be $B (\to b)$ .

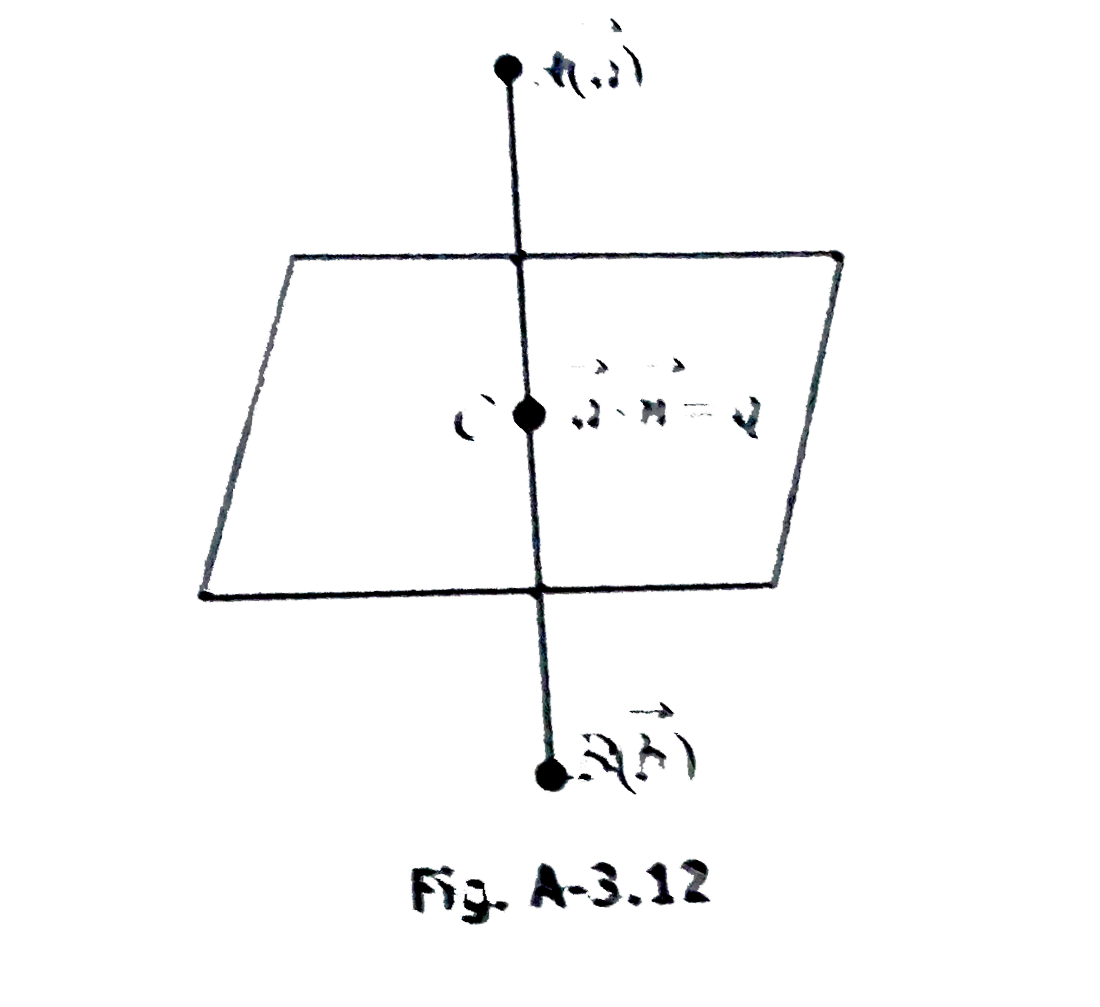
Equation of AC is $\to r = \to a + λ \to n$
( $∵$ AC is normal to the plane) (ii)
Solving (i) and (ii), we get
$(\to a + λ \to n) . \to n = q$
or $λ = \frac{q - \to a . \to n}{{| \to n |}^{2}} . \to n$
But $- - \to O C = \frac{\to a + \to b}{2}$
$∵ \to a + \frac{(q - \to a . \to n) \to n}{{| \to n |}^{2}} = \frac{\to a + \to b}{2}$
or $\to b = \to a + 2 (\frac{q - \to a . \to n}{{| \to n |}^{2}})$

|

Updated on:21/07/2023

Class 12 MATHS THREE DIMENSIONAL GEOMETRY

Topper's Solved these Questions

Similar Questions

CENGAGE-THREE-DIMENSIONAL GEOMETRY -Exercise (Single)

Home
Ask Doubt
Profile