The diagram shows the graph of the derivative of a functin f(x) for 0≤x≤4 with f(0) = 0. Which of the following could be correct statements for y = f(x)?
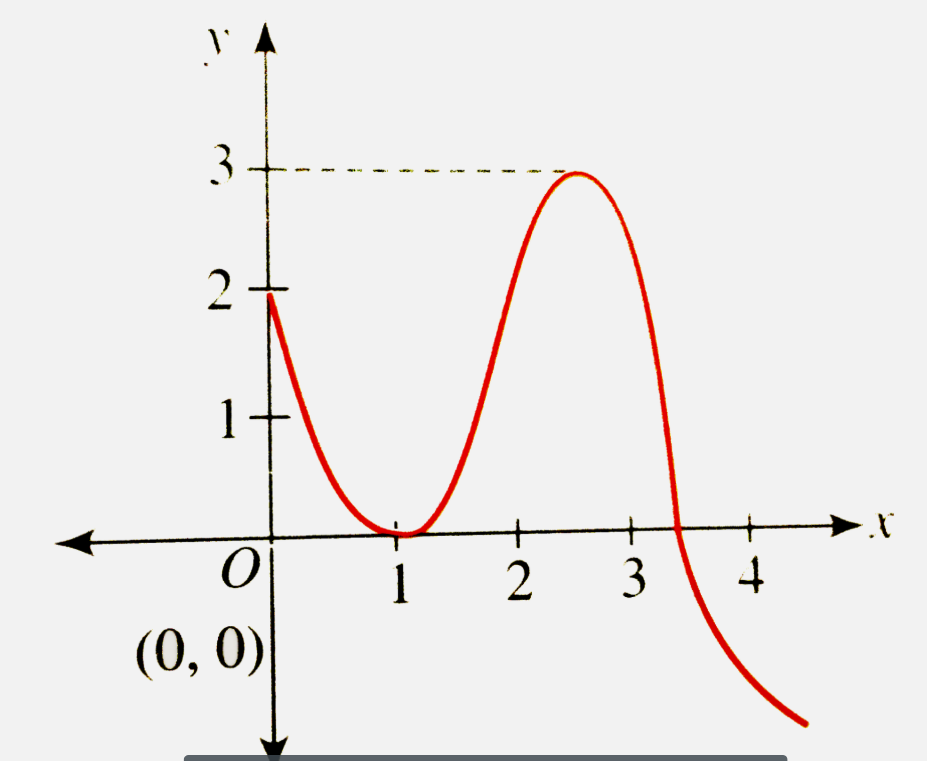
(a) Tangent line to y = f(x) at x = 0 makes an angle of sec−1√5 with the x - axis.
(b) f is increasing in (0, 3).
(c) x = 1 is both an inflection point and the point of local extremum.
(d) Number of critical point on y = f(x) is two. Solution in Tamil
Slope of y tangent at x=0istan−1(2)=sec−1√5.
Hence (a) is correct.
f'(x)≥0 for x∈(0,3), hence f is increasing for (0, 3) , and so (b) is correct.
The x - axis is tangent to the curve at x = 1, therefore f''(1) = 0.
So x = 1 is point of inflection, but not the point of extremum as the sign of f'(x) does not change at x = 1.
Hence (c) is not correct.
Obviously, y = f(x) has two critical points as f'(1) = 0 and f'(3.5) = 0.
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - Exercise18videos
GETTING STARTED WITH GRAPHS
- BOOK - CENGAGECHAPTER - FUNCTIONSEXERCISE - Question Bank21videos
FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise18videos
GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONS
Similar Questions
Does the following graph pass the vertical or horizontal line test ?
 View Solution
View SolutionIf there are four distinct real numbers satisfying thẻ equation ∣∣x2−4x−7∣∣=n, then number of integers in the range of n is
View SolutionDraw the graph of y=tan−1x+cot−1x
01:50View SolutionFollowing is the graph of y = f(x).
(##CENGRAC01S01005_Q01.png width=80%><br>F∈dthes√oftheequation f(x) = 0, f(x) = 4 and f(x) = 10.01:48View SolutionThe diagram shows the graph of the derivative of a functin f(x) for 0≤x≤4 with f(0) = 0. Which of the following could be correct statements for y = f(x)?
(##CENGRAC01S01021_Q01.png width=80%><br>(a)Tan≥ntl∈e→y=f(x)atx=0makesan∠of sec^(-1) sqrt 5 with the x - axis.
(b) f is increasing in (0, 3).
(c) x = 1 is both an inflection point and the point of local extremum.
(d) Number of critical point on y = f(x) is two.View SolutionAt x=0, value of (dy)/(dx) is : ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R04_E01_024_Q01.png" width="80%"gt
05:21View SolutionSuppose f:[−2,2]→R is defined by f(x)={−1 for −2≤x≤0x−1 for 0≤x≤2 , then {x∈[−2,2]:x≤0andf(|x|)=x}=
06:27View SolutionIf f(x)=x2, if 0≤x≤1 =√x, if x≥1,
then area above X-axis, bounded by the line x = 4 and the curve y = f(x) is05:30View SolutionIf f''(x)∣≤1∀x∈R,andf(0)=0=f'(0), then which of the following can not be true ?
02:51View SolutionIf f(x)=x−2,x≤0and4−x2,x>0, then discuss the continuity of y=f(f(x)).
03:03View SolutionThe diagram shows the graph of the derivative of a functin f(x) for 0≤x≤4 with f(0) = 0. Which of the following could be correct statements for y = f(x)?

(a) Tangent line to y = f(x) at x = 0 makes an angle of sec−1√5 with the x - axis.
(b) f is increasing in (0, 3).
(c) x = 1 is both an inflection point and the point of local extremum.
(d) Number of critical point on y = f(x) is two.03:46View Solution|f(x)−f(y)|≤(x−y)2∀x,y∈Randf(0)=1 then
03:01View SolutionIf f(0) = 0 ,f'(0)=2, then the derivative of y=f(f(f(f(x)))) at x = 0 in
02:00View SolutionIf f''(x)∣≤1∀x∈R,andf(0)=0=f'(0), then which of the following can not be true ?
04:21View SolutionIf f(0)=0,f'(0)=2 then what is the derivative of y=f(f(f(f(x)))) at x=0.
02:34View Solution

