A vertical tower stands on a declivity which isinclined at 15∘ to the horizon. From the foot of the tower a man ascends the declivity from 80 feet and then finds that the tower subtends an angle of 30∘. The height of the tower isSolution in Tamil
40(√6+√2)
20(√6−√2)
40(√6−√2)
80(√6−√2)
Let BC be the declivity and BA be the tower .
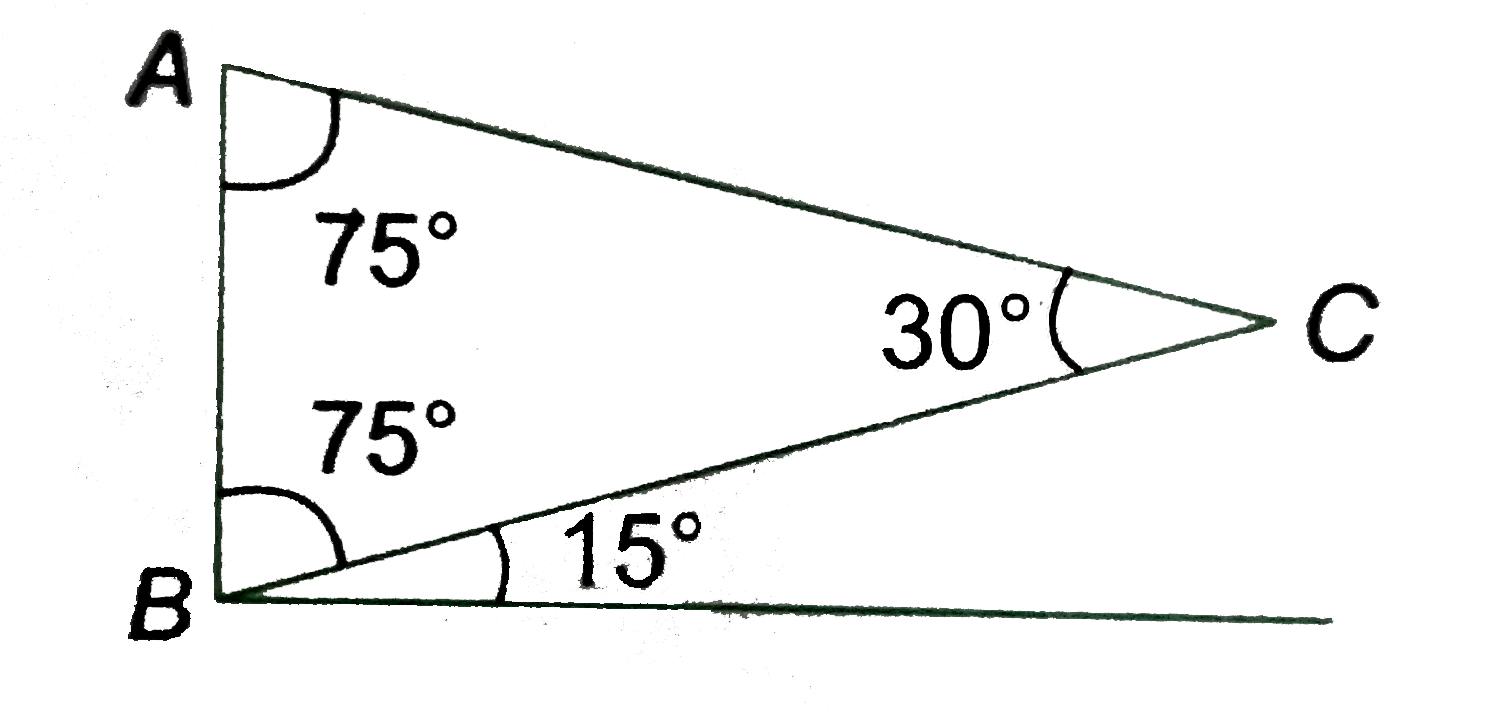
Using sine rule in ΔABC, we get
BCsin75∘=ABsin30∘
⇒AB=80sin30∘sin75∘
⇒AB=40×2√2√3+1=40(√6−√2)
Topper's Solved these Questions
- HIGHT AND DISTANCE BOOK - CENGAGECHAPTER - HIGHT AND DISTANCE EXERCISE - JEE Previous Year
3 Videos
- HIGHT AND DISTANCE BOOK - CENGAGECHAPTER - HIGHT AND DISTANCE EXERCISE - JEE Previous Year
3 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
22 Videos
- HYPERBOLABOOK - CENGAGECHAPTER - HYPERBOLAEXERCISE - JEE Advanced Previous Year
14 Videos
Similar Questions
A bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
View SolutionA bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
View SolutionLet P(6,3) be a point on the hyperbola x2a2−y2b2=1. If the normal at point P intersects the x-axis at (9, 0), then find the eccentricity of the hyperbola.
View SolutionA tower stands vertically on the ground. From a point on the ground, 20m away from the foot of the tower, the angle of elevation of the top of the tower is 60o . What is the height of the tower?
View Solutionधरती पर एक मीनार ऊर्ध्वाधर खड़ी है l धरती के एक बिंदु से , जो मीनार के पाद - बिंदु से 15 m दूर है , मीनार के शिखर का उनंयन कोण 60∘ है l मीनार की ऊँचाई ज्ञात कीजिए l
View Solutionधरती पर एक मीनार ऊर्ध्वाधर खड़ी है । धरती के एक बिन्दु से, जो मीनार के पाद-बिन्दु से 15 मीटर दूर है , मीनार के शिखर का उन्नयन कोण 60∘ है । मीनार की ऊँचाई ज्ञात कीजिए ।
View Solutionएक मीनार जमीन पर उदग्र खड़ा है । मीनार के पाद से 15 m दूर एक बिंदु पर मीनार की चोटी का उन्नमन कोण 60∘ है । मीनार की ऊँचाई क्या है ?
View Solutionएक मीनार के पाद से 40 मीटर दुरी पर स्तिथित किसी बिनु से मीनार के शिखर का उनयन कोण 30∘ है मीनार की उचाई ज्ञात कीजिएः
View SolutionA tower stands at the centre of a circular park . A and B are two points on the boundary of the park such that AB(=a) subtends an angle of 60^@ at the foot of the tower , and the angle of elevation of the top of the tower from A or B is 30^@ . The height of the tower is
View SolutionA vertical tower subtends an angle of 60∘ at a point on the same level as the foot of the tower. On moving 100 m further in line with the tower, it subtends an angle of 30∘ at the point. Then, the height of the tower, it subtends an angle of 30∘ at the point. Then, the height of the tower is
View SolutionA tower stands vertically on the ground. From a point on the ground which is 30 m away from the foot of a tower, the angle of elevation of the top of the tower is found to be 45∘. Find the height of the tower.
View SolutionA tower stands vertically on the ground. From a point on the ground, which is 15 m away from the foot of the tower is found to be 60∘. Find the height of the tower.
View SolutionA tower stands vertically on the ground. From a point on the ground, which is 15maway from the foot of the tower, the angle of elevation of the top of the tower is found to be 60∘. Find the height of the tower.
View SolutionA tower stands at the foot of a hill whose inclination to the horizon is 9∘, at a point 40 m up the hill the tower subtends an angle of 54∘. The height of the tower is
View SolutionA vertical tower stands on a horizontal plane, and from a point on the ground at a distance of 30 metres from the foot of the tower , the angle of elevation is 60∘. The height of the tower is
View Solution
