AB is a vertical pole resting at the end A on the level ground. P is a point on the level ground such that AP = 3AB and C Is the midpoint of AB. If AC and CB subtend angles α and β, respectively, at P, then the value of tanβ is Solution in Tamil
1819
319
16
13
On the basis of the given information , following diagram is obtained .
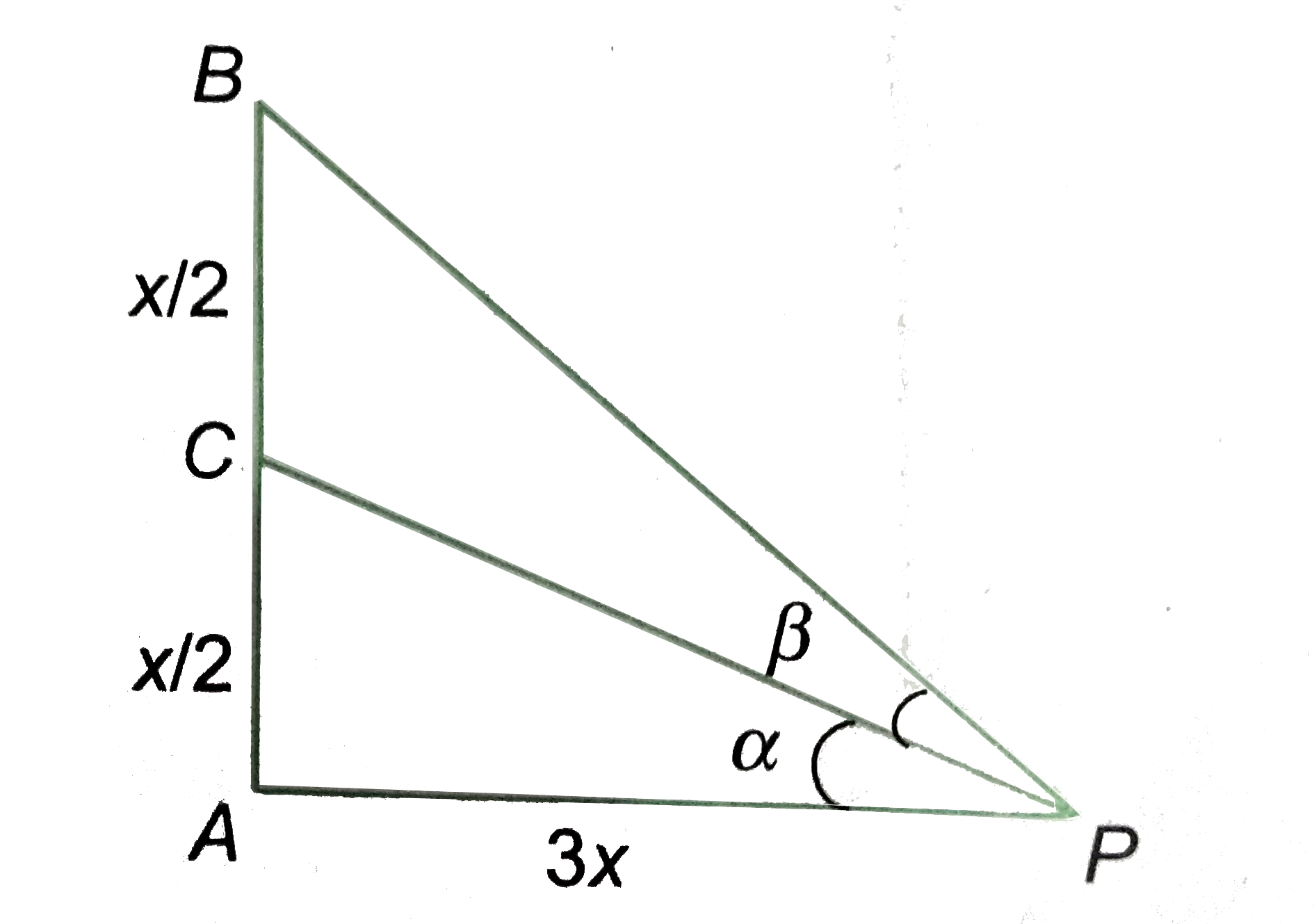
tanβ=tan((α+β)−α)
=13−161+13.16=319
Topper's Solved these Questions
- HIGHT AND DISTANCE BOOK - CENGAGECHAPTER - HIGHT AND DISTANCE EXERCISE - JEE Previous Year
3 Videos
- HIGHT AND DISTANCE BOOK - CENGAGECHAPTER - HIGHT AND DISTANCE EXERCISE - JEE Previous Year
3 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
22 Videos
- HYPERBOLABOOK - CENGAGECHAPTER - HYPERBOLAEXERCISE - JEE Advanced Previous Year
14 Videos
Similar Questions
A bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
View SolutionA bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
View SolutionLet P(6,3) be a point on the hyperbola x2a2−y2b2=1. If the normal at point P intersects the x-axis at (9, 0), then find the eccentricity of the hyperbola.
View SolutionAB is a vertical pole resting at the end A on the level ground. P is a point on the level ground such that AP = 3AB and C Is the midpoint of AB. If AC and CB subtend angles α and β, respectively, at P, then the value of tanβ is
View SolutionLet a vertical tower AB have its end A on the level ground. Let C be the mid-point of AB and P be a point on the ground such that AP = 2AB. If √BPC=β, then tan β is equal to
View SolutionAB is a vertical pole. The end A is on the level ground .C is the middle point of AB. P is a point on the level ground . The portion BC subtends an angles beta at P. If AP = nAB, then tan beta =
View SolutionAB is a vertical pole and C is its mid point. The end A is on the level ground and P is any point on the level ground other than A the portion CB substends an angle β at P. If AP:AB=2:1, then β=
View SolutionA vertical pole subtends an angle Tan−1(12) at a point P on the ground. IF the angles subtended by the upper half and the lower half of the pole at P are respectively αandβ, then (tanα,tanβ)=
View SolutionAB एक ऊर्ध्वाधर खम्भा है | सिरा 'A' एक समतल मैदान पर है | C, AB का मध्य - बिन्दु है | समतल मैदान पर एक बिन्दु P है | भाग CB, बिन्दु P पर कोण β बनाता है | यदि AP = nAB तो दिखाइए कि tanβ=n2n2+1
View Solutionমনে করো, AB একটি টাওয়ার যার A প্রান্তটি ভূমির ওপর অবস্থিত। মনে করো, C,AB এর মধ্যবিন্দু এবং ভূমির ওপর অবস্থিত P একটি বিন্দু যেখানে AP=2AB। যদি ∠BPC=β হয়, তাহলে tanβ=
View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी हैं कि उसका सिरा A भूमि पर हैं। माना AB का मध्य-बिन्दु C हैं तथा भूमि पर स्थिर बिन्दु P ऐसा हैं कि AP = 2 AB| यदि ∠BPC=β हैं, तो tanβ बराबर हैं
View SolutionAB is a vertical pole resting at the end A on the level ground. P is a point on the level ground such that AP = 3AB and C Is the midpoint of AB. If AC and CB subtend angles α and β, respectively, at P, then the value of tanβ is
View SolutionAB is a vertical pillar that stands on the earth surface A. Another point on the earth surface is p such that AP = 3AB if the midpoint of AB is C and on CB. beta Who transfers? tan beta The value of.
View SolutionA vertical pole subtends an angle Tan−1(12) at a point P on the ground. On the ground .If the angles subtends by the upper half and the lower half of the pole at P are respectively αandβ then (tanα,tanβ)
View Solution
