Whether the given equation ? Solution in Tamil
(i) We have
Now
The sign scheme of is as follows.

So is the point of minima and is the point of maxima.
and
Hence the graph of the function is as shown in the following figure.

As shown in the figure, the graph cute the x-axis at three distinct points.
Hence the equation has three distinct roots.
(ii) We have
and
Also
Hence the graph of is as shown in the following figure.
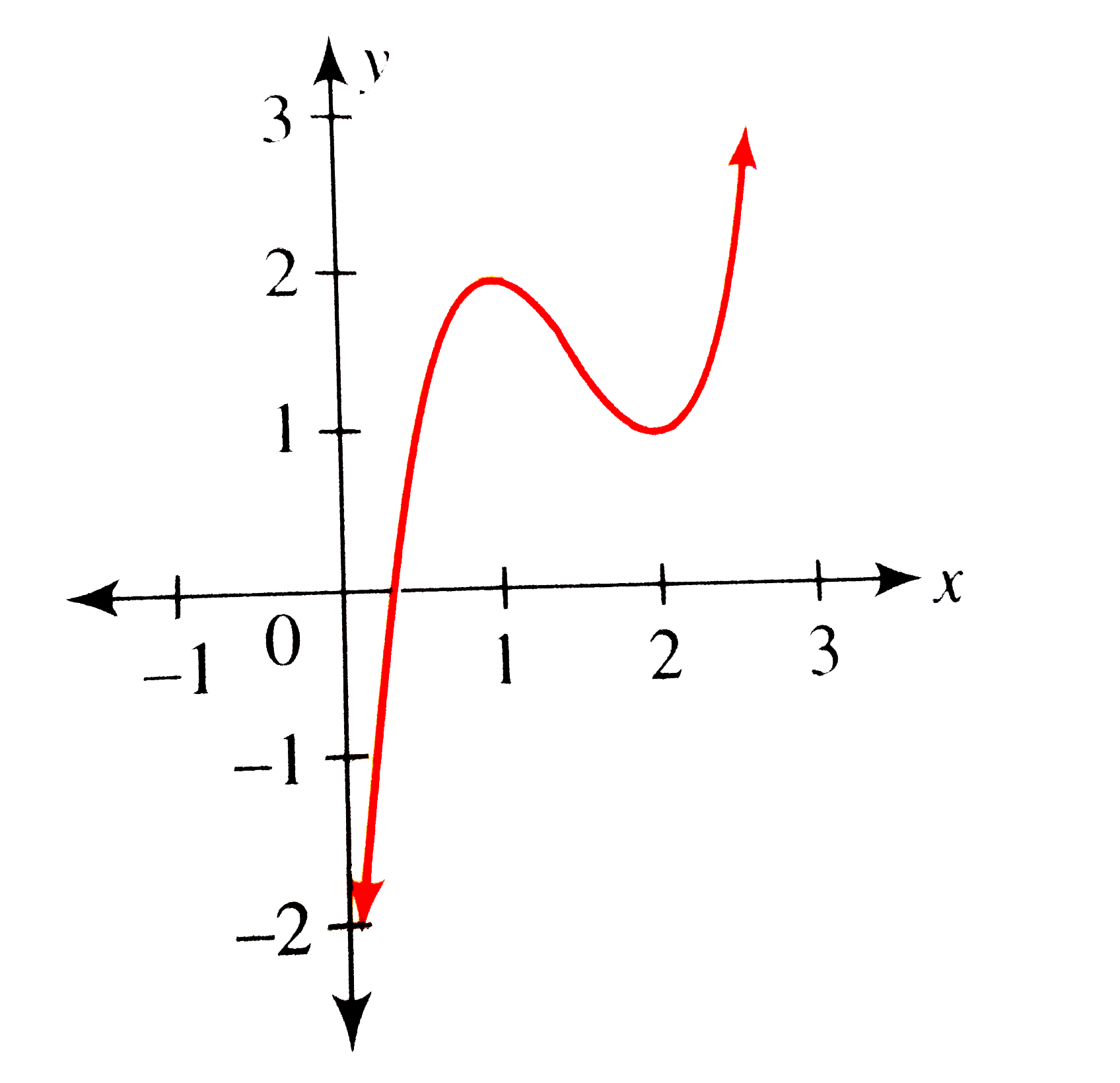
Thus, from the graph we can see that has only one real root, though has two turning points.
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercise13videos
GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises4videos
GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise14videos
GRAPHICAL TRANSFORMATIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise34videos
GRAPHS OF ELEMENTARY FUNCTIONS
Similar Questions
Draw the graph of y=(x−1)(x2−x+1).
03:36View SolutionSketch the graph of an example of a rational function f that satisfies all the given conditions.
(i) f(0)=0,f(1),limx→∞f(x)=0,f is odd
(ii) limx→0+f(x)=∞,limx→0−f(x)=−∞,limx→∞f(x)=1,limx→−∞f(x)=1
(iii) limx→−2f(x)=∞,limx→−∞f(x)=3,limx→∞f(x)=3,f(0)=002:54View SolutionDraw the graph of y=tan−1x−cot−1x.
03:06View SolutionDraw the graph of y=1(1/x).
03:01View Solution(1+tanθ+secθ)( 1+cotθ−cosec θ )= (a) 0 (b) 2 (c) 1 (d) −1
02:16View Solutioncosθ1−tanθ + sinθ1−cotθ is equals to
03:16View Solution√1+sinθ1−sinθ is equal to
(a)secθ+tanθ
(b) secθ−tanθ
(c) sec 2 θ+ tan 2 θ
(d) sec 2 θ− tan 2 θ04:01View Solution(1+tanθ+secθ)( 1+cotθ−cosec θ )= (a) 0 (b) 2 (c) 1 (d) −1
02:19View SolutionIf tanθ+secθ=√3,0 <θ<π, then θ is equal to a. 5π6 b. 2π3 c. π6 d. π3
03:57View SolutionProve that (secθ−tanθ)2=1−sinθ1+sinθ
03:09View SolutionIf ((sinθ−cosecθ)(cosθ−secθ))/(tan^(2)θ -sin^(2)θ) = r^3 , then r=? यदि ((sinθ−cosecθ)(cosθ−secθ))/(tan^(2)θ -sin^(2)θ) = r^3 है तो r बराबर हैः
03:04View Solution(1−tanθ1−cotθ)2+1 = ? (1−tanθ1−cotθ)2+1 बराबर है :
01:26View SolutionIf secθ+tanθ=p, (p>1) ,then cosecθ+1cosecθ−1 = ? यदि secθ+tanθ=p, (p>1) ,तो cosecθ+1cosecθ−1 = ? का मान क्या है?
04:53View SolutionThe value of (1+cotθ–cosecθ)(1+cosθ+sinθ)secθ = ? (1+cotθ–cosecθ)(1+cosθ+sinθ)secθ का मान है :
04:27View SolutionIf (sinθ1+cosθ)+(1+cosθsinθ)=4√3 0∘<θ<90∘, then the value of (tanθ+secθ)−1 is : यदि (sinθ1+cosθ)+(1+cosθsinθ)=4√3 0∘<θ<90∘,, तो (tanθ+secθ)−1 का मान है :
02:43View Solution

