A vertex of an equilateral triangle is $2, 3$ and the opposite side is $x + y = 2 .$ Find the equations of other sides.

Text Solution

Verified by Experts

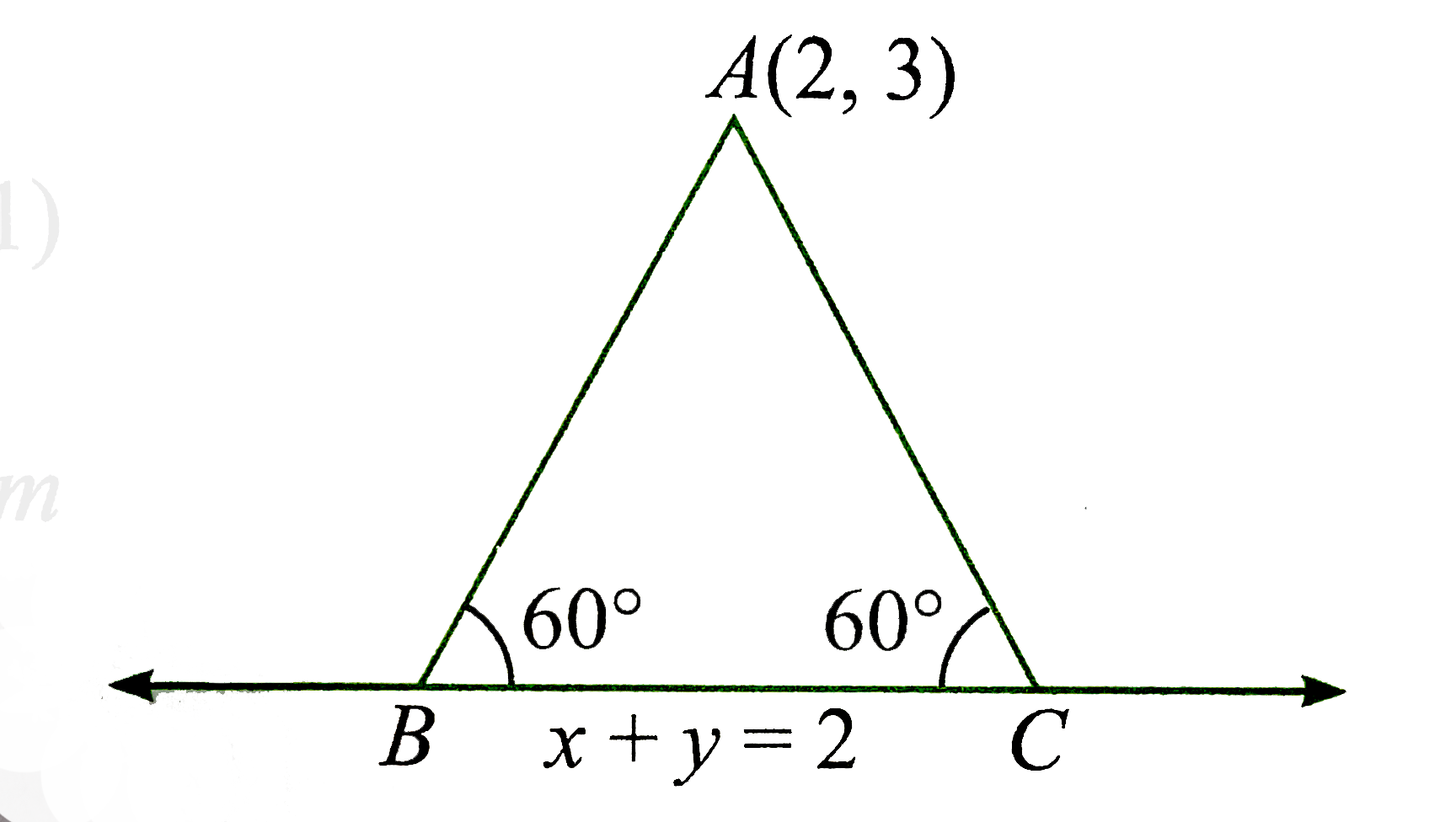
Given line is
$x + y - 2 = 0 (1)$
Its slope is $m_{1} = - 1$
Let the slope of the line be m which makes an angle of $60^{\circ}$ with line in (1). Then,
${tan 60}^{\circ} = ∣ ∣ ∣ \frac{m_{1} - m}{1 + m_{1} m} ∣ ∣ ∣ or \sqrt{3} = ∣ ∣ ∣ \frac{- 1 - m}{1 - m} ∣ ∣ ∣$
$or \sqrt{3} = ∣ ∣ ∣ \frac{1 + m}{m - 1} ∣ ∣ ∣ or \frac{1 + m}{m - 1} = \pm \sqrt{3}$
$or 1 + m = \pm \sqrt{3} (m - 1)$
$or m = \frac{\sqrt{3} + 1}{\sqrt{3} - 1}, \frac{\sqrt{3} - 1}{\sqrt{3} + 1}$
$= 2 + \sqrt{3}, 2 - \sqrt{3}$
Therefore, the equations of other two sides of the triangle are
$y - 3 = (2 + \sqrt{3}) (x - 2)$
$and y - 3 = (2 - \sqrt{3}) (x - 2)$

Updated on:21/07/2023