Find the straight line passing through the point of intersection of lines 2x+3y+5=0 and 5x-2y-16=0 and through the point (-1,3) using the concept of family of lines. Solution in Tamil

Video Solution

Text Solution

Verified by Experts

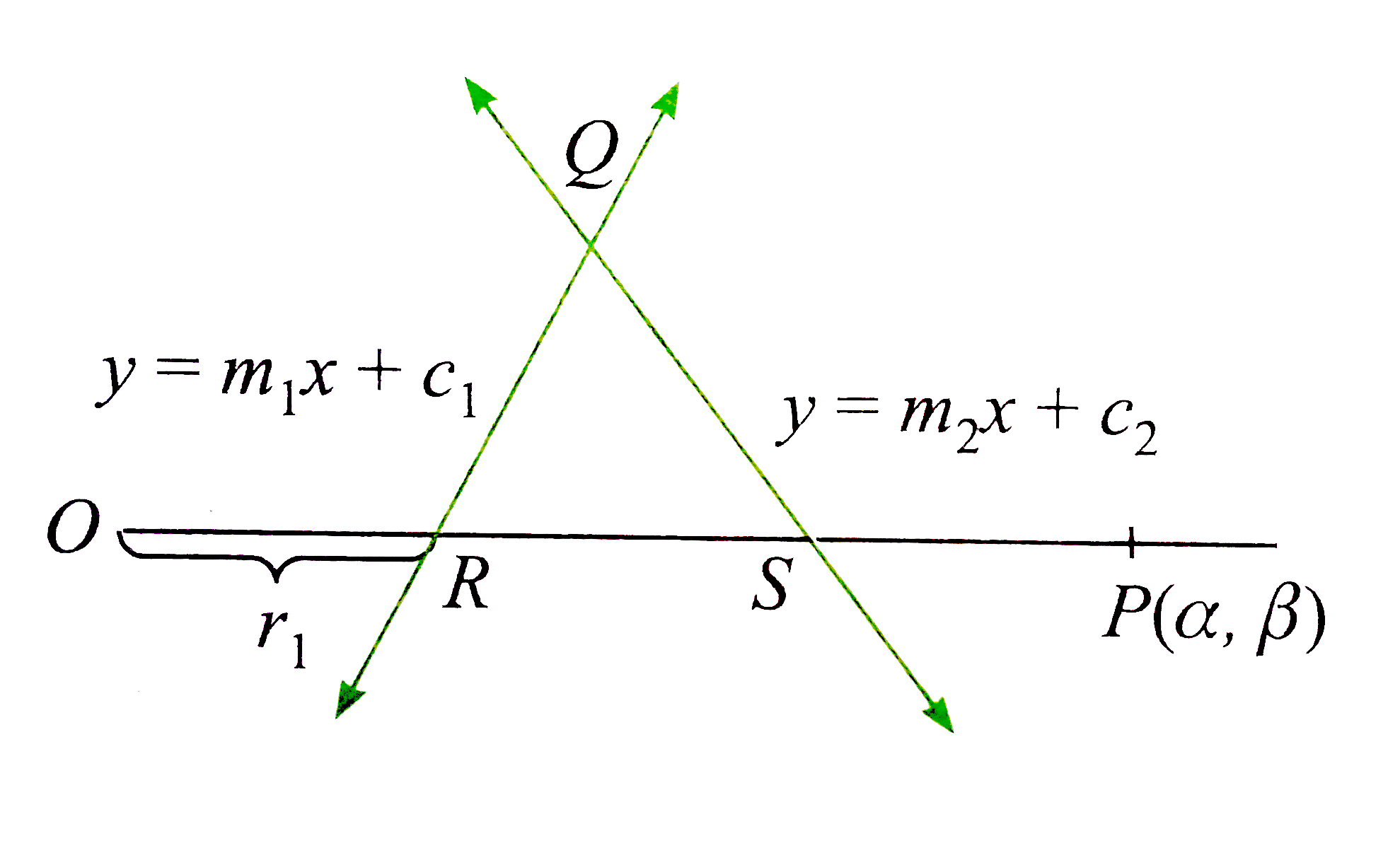
Let the variable line through O makes an angle $θ$ with the positive direction of the x-axis. Any point on this variable line is $(O + r cos θ, 0 + r sin θ)$
$i . e ., (r cos θ, r sin θ)$
Let the fixed lines be
$y = m_{1} x + c_{1} (1)$
$and y = m_{2} x + c_{2} (2)$
$Let O R = r_{1}, O S = r_{2}, O P = r_{3} .$ So, according to the equation,
$\frac{m + n}{r_{3}} = \frac{m}{r_{1}} + \frac{m}{r_{2}} (3)$
Since R and S lie on lines (1) and (2), respectively, we have
$r_{1} sin θ = m_{1} (r_{1} cos θ) + c_{1} (4)$
$and r_{2} sin θ = m_{2} (r_{2} cos θ) + c_{2} (5)$
$Let P \equiv (α, β) . Then,$
$α = r_{3} cos θ, β = r_{3} sin θ (6)$
From (3), (4), and (5), we have
$\frac{m + n}{r_{3}} = m \frac{sin θ - m_{1} cos θ}{c_{1}} = + n \frac{sin θ - m_{2} cos θ}{c_{2}}$ ltrgt $or m + n = \frac{m}{c_{1}} (β - m_{1} α) + \frac{n}{c_{2}} (β - m_{2} α) [F r o m (6)]$
Hence, the locus of P is
$m + n = (\frac{m}{c_{1}} + \frac{n}{c_{2}}) y - (\frac{m m_{1}}{c_{1}} + \frac{n m_{2}}{c_{2}}) x$
$or y - m_{1} x - c_{1} + \frac{n}{m} \frac{c_{1}}{c_{2}} (y - m_{2} x - c_{2}) = 0 (7)$
Clearly, the locus of P is a straight line passing through the point of intersection of the given lines (1) and (2).

|

Updated on:21/07/2023

Class 12 MATHS STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

CENGAGE-STRAIGHT LINES-JEE Advanced Previous Year

Home
Ask Doubt
Profile