about to only mathematics Solution in Tamil

Video Solution

Text Solution

Verified by Experts

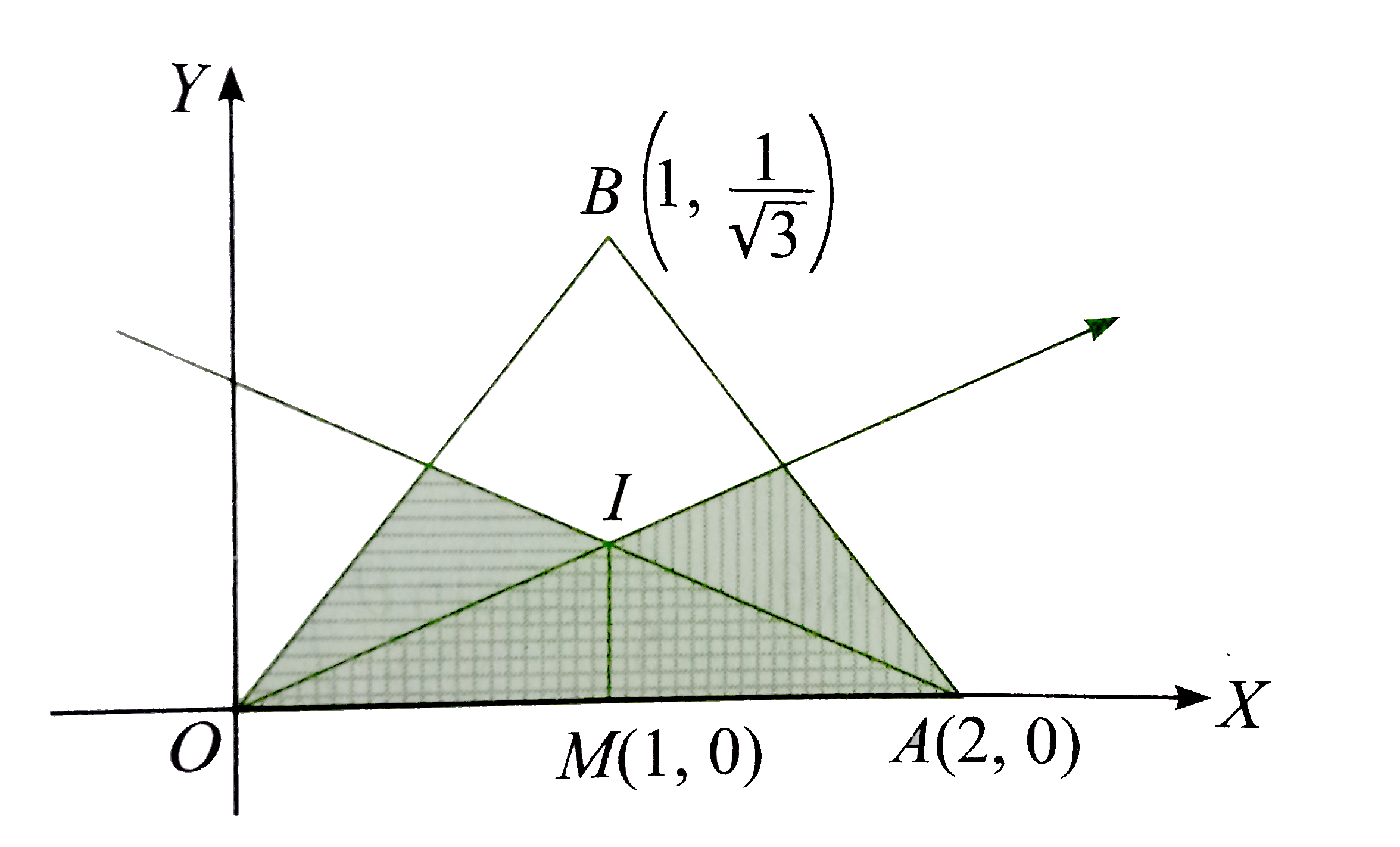
$d (P, O A) \leq min [d (P, O B), d (P, A B)],$
$\Rightarrow d (P, O A) \leq d (P, O B) and d (P, O A) \leq d (P, A B),$
When d(P,OA)= d(P,OB), P is equidistant from OA and OB, i.e., P lies on angle bisector of lines OA and OB.
So, when $d (P, O A) < d (P, O B)$ , Point P is nearer to OA than to OB, i.e., it lies below bisector of OA and oB.
Similarly, when $d (P, O A) < d (P, A B)$ P is nearer to OA than to AB, i.e., it lies below bisector of OA and AB.
Common region satisfied by these two inequalities is the region formed by two bisectors and OA, i.e., triangle OIA.
$∴ Required area = Area of triangle OIA$
$Now, ∠ B O A = \frac{1 / \sqrt{3}}{1} = \frac{1}{\sqrt{3}}$
$∴ ∠ B O A = 30^{\circ}$
$\Rightarrow ∠ I O A = 15^{\circ}$
$\Rightarrow I M = tan 15^{\circ} = 2 - \sqrt{3}$
$∴ Area of triangle OIA = \frac{1}{2} \times O A \times I M$
$= \frac{1}{2} \times 2 \times (2 - \sqrt{3}) = 2 - \sqrt{3} sq. units$

|

Updated on:21/07/2023

Class 12 MATHS STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

CENGAGE-STRAIGHT LINES-JEE Advanced Previous Year

Home
Ask Doubt
Profile