A beam of light is sent along the line x−y=1 , which after refracting from the x-axis enters the opposite side by turning through 300 towards the normal at the point of incidence on the x-axis. Then the equation of the refracted ray is (2−√3)x−y=2+√3 (2+√3)x−y=2+√3 (2−√3)x+y=(2+√3) y=(2−√3)(x−1)Solution in Tamil
(2−√3)x−y=2+√3
(2+√3)x−y=2+√3
(2−√3)x+y=(2+√3)
y=(2+√3)(x−1)
The correct Answer is:D
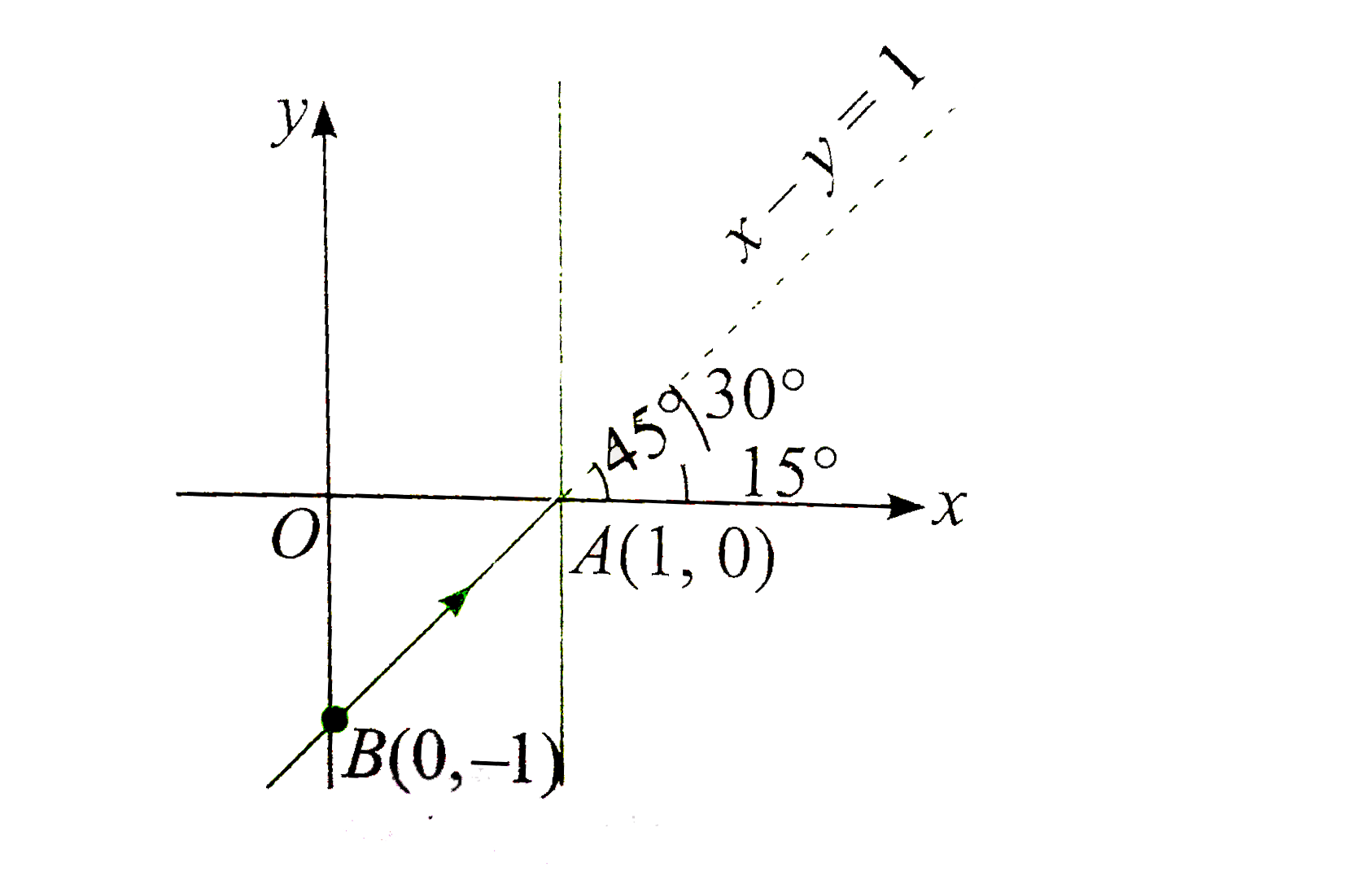
From the figure, the refracted ray makes and angle of 15∘ with the positive direction of the x-axis and passes through the point (1,0). Its equation is
(y−0)=(tan15∘)(x−1)
or y=(2−√3)(x−1)
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Multiple)30videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Comprehension)27videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.65videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year9videos
THEORY OF EQUATIONS
Similar Questions
If P is a point (x,y) on the line y=−3x such that P and the point (3, 4) are on the opposite sides of the line 3x−4y=8, then x>815 (b) x>85 y<−85 (d) y<−815
04:29View SolutionLet L be the line belonging to the family of straight lines (a+2b) x+(a-3b)y+a-8b =0, a, b ∈R, which is the farthest from the point (2, 2).
Area enclosed by the line L and the coordinate axes is03:22View SolutionIf aandb are two arbitrary constants, then prove that the straight line (a−2b)x+(a+3b)y+3a+4b=0 will pass through a fixed point. Find that point.
02:18View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
02:14View SolutionQ. Let p and q real number such that p≠0,p2≠q and p2≠−q. if α and β are non-zero complex number satisfying α+β=−p and α3+β3=q, then a quadratic equation having αβ and βα as its roots is
07:13View SolutionA beam of light is sent along the line x−y=1 , which after refracting from the x-axis enters the opposite side by turning through 300 towards the normal at the point of incidence on the x-axis. Then the equation of the refracted ray is (a) (2−√3)x−y=2+√3 (b) (2+√3)x−y=2+√3 (c) (2−√3)x+y=(2+√3) (d) y=(2−√3)(x−1)
19:32View SolutionThe equation of the common tangent touching the circle (x−3)2+y2=9 and the parabola y2=4x above the x-axis is √3y=3x+1 (b) √3y=−(x+3) (C)√3y=x+3 (d) √3y=−(3x−1)
05:14View SolutionThe equation of tangent to the curve y=∫x3x2dt√1+t2 at x=1 is √3x+1=y (b) √2y+1=x √3x+y=1 (d) √2y=x
02:58View Solutionif x=sqrt(3)+(1)/(sqrt(3)) and y=sqrt(3)-(1)/(sqrt(3)) then x^(2)-y^(2) is
06:45View SolutionA vertex of an equilateral triangle is at (2, 3), and th equation of the opposite side is x+y=2, then the equaiton of the other two sides are (A) y=(2+√3)(x−2),y−3=2√3(x−2) (B) y−3=(2+√3(x−2),y−3=(2−√3(x−2) (C) y+3=(2−√3(x−2),y−3=(2−√3(x+2) (D) none of these
04:40View SolutionA circle C of radius 1 is inscribed in an equilateral triangle PQR. The points of contact of C with the sides PQ,QR,RPandD,E,F respectively. The line PQ is given by the equation √3+y−6=0 and the point D is (√32,32). Equation of the sides QR,RP are : (A) y=2√3x+1,y=2√3x−1 (B) y=1√3x,y=0 (C) y=√32x+1,y=√32x−1 (D) y=√3x,y=0
06:31View Solutionयदि x=√3+1√3−1 & y=√3−1√3+1, है तो x2+y2 का मान क्या होगा?
05:38View SolutionIf x=(sqrt(3)+1)/(sqrt(3)-1) and y=(sqrt(3)-1)/(sqrt(3)+1) then find the value of x^(2)+y^(2)
04:38View Solutionयदि x=√3−√2√3+√2 व y=√3+√2√3−√2, तब निम्न के मान ज्ञात कीजिए - x3+y3
03:25View Solutionयदि x=√3+√2√3−√2 व y=1x, तब सिद्ध कीजिए कि x2+y2+xy=99
04:02View Solutionx=√3+1√3−1 এবং y=√3−1√3+1 হয়, তবে দেখাও যে, x2+y2x2−y2=7√312
09:28View Solution

