A triangle is formed by the lines $x + y = 0, x - y = 0,$ and $l x + m y = 1 .$ If $l a n d m$ vary subject to the condition $l^{2} + m^{2} = 1,$ then the locus of its circumcenter is ${(x^{2} - y^{2})}^{2} = x^{2} + y^{2}$ ${(x^{2} + y^{2})}^{2} = (x^{2} - y^{2})$ ${(x^{2} + y^{2})}^{2} = 4 x^{2} y^{2}$ ${(x^{2} - y^{2})}^{2} = {(x^{2} + y^{2})}^{2}$ Solution in Tamil

A

${(x^{2} - y^{2})}^{2} = x^{2} + y^{2}$

B

${(x^{2} - y^{2})}^{2} = (x^{2} - y^{2})$

C

$(x^{2} - y^{2}) = 4 x^{2} y^{2}$

D

${(x^{2} - y^{2})}^{2} = {(x^{2} + y^{2})}^{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

The coordinates of circumcenter are $(l / (l^{2} - m^{2}), m / (m^{2} - l^{2})) .$
Hence,
$h = \frac{l}{l^{2} - m^{2}} (1)$
$k = - \frac{m}{l^{2} - m^{2}} (2)$

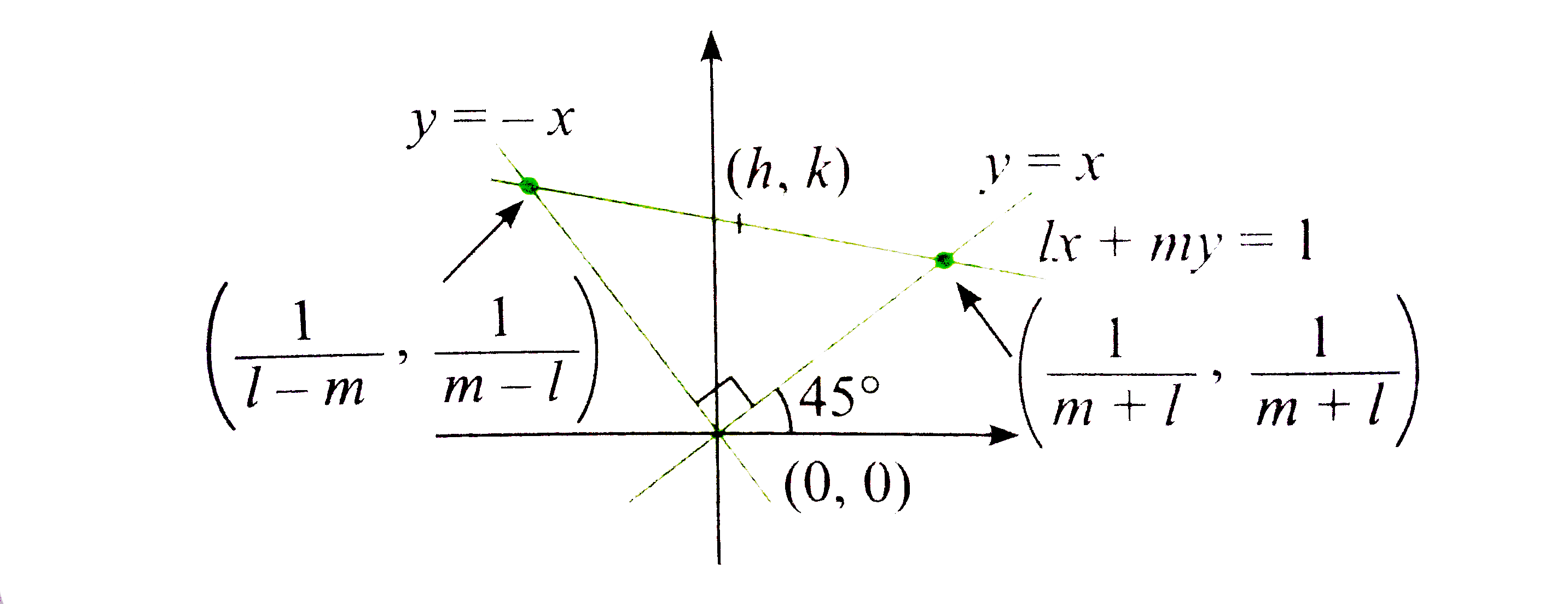
Squaring and adding (1) and (2), we get
$h^{2} + k^{2} = \frac{l^{2} + m^{2}}{{(l^{2} - m^{2})}^{2}} = \frac{1}{{(l^{2} - m^{2})}^{2}} (Putting l^{2} + m^{2} = 1)$
$Also, h^{2} - k^{2} = \frac{1}{l^{2} - m^{2}}$
Therefore, the locus is $x^{2} + y^{2} = {(x^{2} - y^{2})}^{2}$ .

Updated on:21/07/2023

|

Class 12 MATHS STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

CENGAGE-STRAIGHT LINES-Exercise (Single)

Home
Ask Doubt
Profile