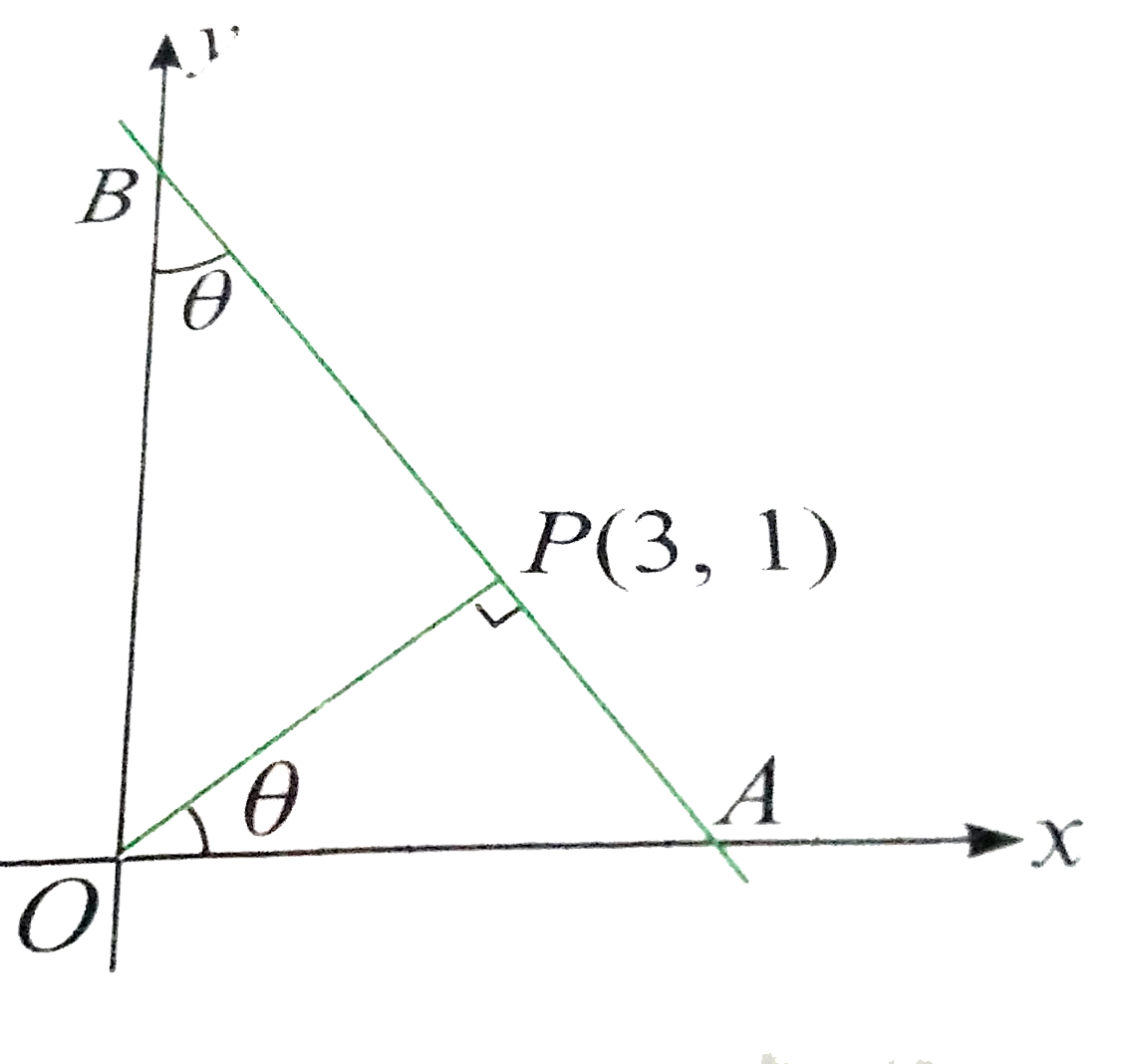
A straight line passing through P(3,1) meets the coordinate axes at AandB . It is given that the distance of this straight line from the origin O is maximum. The area of triangle OAB is equal to 503sq.units (b) 253sq.units 203sq.units (d) 1003sq.unitsSolution in Tamil
50/3 sq.units
25/3 sq.units
20/3 sq.units
100/3 sq.units
The correct Answer is:A
Line AB will be the farthest from the origin if OP is right angled to the line drawn.
OP=√10
Also, tanθ=13
OA=OPsecθ
=√10×√103=10
OB=OPcosecθ=√10×√101=10
∴ Area of ΔOAB=12=12(103(10)=503
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise (Multiple)13videos
COORDINATE SYSYEM
- BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise (Comprehension)10videos
COORDINATE SYSYEM
- BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.69videos
COORDINATE SYSYEM
- BOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type2videos
COORDINATE SYSTEM
- BOOK - CENGAGECHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.213videos
CROSS PRODUCTS
Similar Questions
If (−6,−4),(3,5),(−2,1) are the vertices of a parallelogram, then the remaining vertex can be (0,−1) (b) 7,9) (−1,0) (d) (−11,−8)
05:44View SolutionStudy the diagram. The line l is perpendicular to line m Does PE bisect CG?
06:05View SolutionFind the locus of a point whose distance from (a, 0) is equal to its distance from the y-axis.
08:39View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
06:56View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
08:00View SolutionLet f(x)=x3+3x+2andg(x) be the inverse of it. Then the area bounded by g(x) , the x-axis, and the ordinate at x=−2andx=6 is 14sq.units (b) 43sq.units 54sq.units (d) 73sq.units
02:45View SolutionThe area of the region enclosed between the curves x=y2−1andx=|y|√1−y2 is 1sq.units (b) 43sq.units 23sq.units (d) 2sq.units
05:21View SolutionThe area of the closed figure bounded by x=−1,x=2,and y={−x2+2,x≤12x−1,x>1andtheabscissaaξsis 163sq.units (b) 103sq.units 133sq.units (d) 73sq.units
05:22View SolutionThe area bounded by the curve a2y=x2(x+a) and the x-axis is a23sq.units (b) a24sq.units 3a24sq.units (d) a212sq.units
07:59View SolutionA straight line passing through P(3,1) meets the coordinate axes at AandB . It is given that the distance of this straight line from the origin O is maximum. The area of triangle OAB is equal to 503sq.units (b) 253sq.units 203sq.units (d) 1003sq.units
06:28View SolutionA tangent having slope of −43 to the ellipse x218+y232=1 intersects the major and minor axes at point AandB, respectively. If C is the center of the ellipse, then the area of triangle ABC is 12sq.units (b) 24sq.units 36sq.units (d) 48sq.units
05:10View SolutionThe line 2x+3y=12 meets the x-axis at A and the y-axis at B . The line through (5, 5) perpendicular to AB meets the x-axis, y-axis & the line AB at C,D,E respectively. If O is the origin, then the area of the OCEB is
(a) 203squnit
(b) 233squnit
(c) 263squnit
(d) 5√529squnit04:59View SolutionThe area bounded by the curve y2=8x and x2=8y is 163sq.units b. 316sq.units c. 143sq.units d. 314sq.units
04:52View SolutionLet f(x)=x3+3x+2andg(x) be the inverse of it. Then the area bounded by g(x) , the x-axis, and the ordinate at x=−2andx=6 is (a) 94sq.units (b) 43sq.units (c) 54sq.units (d) 73sq.units
05:57View SolutionThe area bounded by the loop of the curve 4y2=x2(4−x2) is (a)7/3 sq. units (b) 83sq.unites 113sq.units (d) 163sq.units
03:39View SolutionThe area of the closed figure bounded by x=−1,x=2,and y={−x2+2,x≤12x−1,x>1and the ascissa axis is (a)163sq.units (b) 103sq.units (c)133sq.units (d) 73sq.units
02:50View Solution

