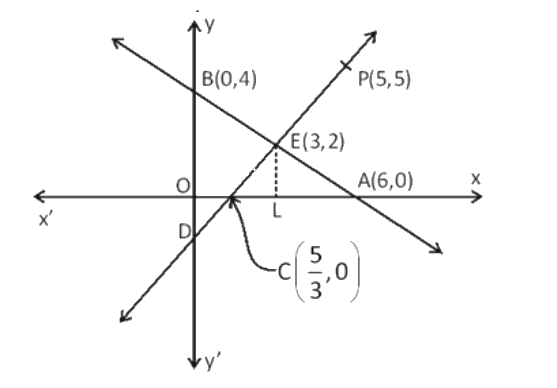
The line 2x+3y=12 meets the x-axis at A and the y-axis at B . The line through (5, 5) perpendicular to AB meets the x-axis, y-axis & the line AB at C,D,E respectively. If O is the origin, then the area of the OCEB is
(a) 203squnit
(b) 233squnit
(c) 263squnit
(d) 5√529squnit
To solve the problem step by step, we will follow these steps:
Step 1: Find the points A and B where the line meets the axes.
The line given is 2x+3y=12.
- Finding point A (x-intercept): Set y=0:
2x+3(0)=12⟹2x=12⟹x=6
Thus, A(6,0).
- Finding point B (y-intercept): Set x=0:
2(0)+3y=12⟹3y=12⟹y=4
Thus, B(0,4).
Step 2: Determine the slope of line AB.
The slope m of line segment AB can be calculated using the coordinates of points A and B:
mAB=y2−y1x2−x1=4−00−6=−23
Step 3: Find the slope of the line perpendicular to AB.
The slope of the line perpendicular to AB is the negative reciprocal of mAB:
mDE=32
Step 4: Write the equation of the line DE passing through point (5, 5).
Using the point-slope form of the line equation:
y−y1=m(x−x1)⟹y−5=32(x−5)
Simplifying this:
y−5=32x−152⟹2y−10=3x−15⟹2y=3x−5⟹3x−2y−5=0
Step 5: Find the intersection points C, D, and E.
- Finding point C (intersection with x-axis): Set y=0:
3x−2(0)−5=0⟹3x=5⟹x=53
Thus, C(53,0).
- Finding point D (intersection with y-axis): Set x=0:
3(0)−2y−5=0⟹−2y=5⟹y=−52
Thus, D(0,−52).
- Finding point E (intersection with line AB): Substitute y from the line DE into the line AB:
2x+3(32x−52)=12
Simplifying:
2x+92x−152=12⟹4x+9x−152=12⟹13x−15=24⟹13x=39⟹x=3
Substitute x=3 back into the equation of line DE to find y:
y=32(3)−152=9−152=−3
Thus, E(3,−3).
Step 6: Calculate the area of quadrilateral OCEB.
We can use the formula for the area of a polygon given by its vertices:
Area=12|x1y2+x2y3+x3y4+x4y1−(y1x2+y2x3+y3x4+y4x1)|
Substituting the coordinates O(0,0), C(53,0), E(3,−3), B(0,4):
Area=12∣∣∣0⋅0+53⋅(−3)+3⋅4+0⋅0−(0⋅53+0⋅3+(−3)⋅0+4⋅0)∣∣∣
Calculating:
=12|0−5+12+0|=12|7|=72
Step 7: Final area calculation.
Now we need to calculate the area of triangle OCEB:
1. Area of triangle OCE:
AreaOCE=12×base×height=12×53×3=52
2. Area of triangle OBE:
AreaOBE=12×base×height=12×3×4=6
3. Total area OCEB:
AreaOCEB=AreaOCE+AreaOBE=52+6=52+122=172
Conclusion
The area of quadrilateral OCEB is 233 square units.
The line given is 2x+3y=12.
2x+3(0)=12⟹2x=12⟹x=6
Thus, A(6,0).
2(0)+3y=12⟹3y=12⟹y=4
Thus, B(0,4).
The slope m of line segment AB can be calculated using the coordinates of points A and B:
mAB=y2−y1x2−x1=4−00−6=−23
The slope of the line perpendicular to AB is the negative reciprocal of mAB:
mDE=32
Using the point-slope form of the line equation:
y−y1=m(x−x1)⟹y−5=32(x−5)
Simplifying this:
y−5=32x−152⟹2y−10=3x−15⟹2y=3x−5⟹3x−2y−5=0
- Finding point C (intersection with x-axis): Set y=0:
3x−2(0)−5=0⟹3x=5⟹x=53
Thus, C(53,0).
3(0)−2y−5=0⟹−2y=5⟹y=−52
Thus, D(0,−52).
2x+3(32x−52)=12
Simplifying:
2x+92x−152=12⟹4x+9x−152=12⟹13x−15=24⟹13x=39⟹x=3
Substitute x=3 back into the equation of line DE to find y:
y=32(3)−152=9−152=−3
Thus, E(3,−3).
We can use the formula for the area of a polygon given by its vertices:
Area=12|x1y2+x2y3+x3y4+x4y1−(y1x2+y2x3+y3x4+y4x1)|
Substituting the coordinates O(0,0), C(53,0), E(3,−3), B(0,4):
Area=12∣∣∣0⋅0+53⋅(−3)+3⋅4+0⋅0−(0⋅53+0⋅3+(−3)⋅0+4⋅0)∣∣∣
Calculating:
=12|0−5+12+0|=12|7|=72
Now we need to calculate the area of triangle OCEB:
1. Area of triangle OCE:
AreaOCE=12×base×height=12×53×3=52
2. Area of triangle OBE:
AreaOBE=12×base×height=12×3×4=6
3. Total area OCEB:
AreaOCEB=AreaOCE+AreaOBE=52+6=52+122=172
The area of quadrilateral OCEB is 233 square units.
Topper's Solved these Questions
Similar Questions
The line 2x+3y=12 meets the x-axis at A and the y-axis at B . The line through (5, 5) perpendicular to AB meets the x-axis, y-axis & the line AB at C,D,E respectively. If O is the origin, then the area of the OCEB is
(a) 203squnit
(b) 233squnit
(c) 263squnit
(d) 5√529squnit
View SolutionThe line 2x+3y=12 meets the x-axis at A and y-axis at B. The line through (5,5) perpendicular to AB meets the x-axis and the line AB at C and E respectively. If O is the origin of coordinates, find the area of figure OCEB.
View Solution
Knowledge Check
Line 3x + 2y =24 meets x-axis at A and y- axis at B and perpending bisector of AB meets the line passing through (0,1) and parallel to x-axis at C. Area of ΔABC is
A182 sq unitsB91 sq unitsC48 sq unitsDnone of these
The line 2x+3y=12 meets the coordinates axes at A and B respectively. The line through (5, 5) perpendicular to AB meets the coordinate axes and the line AB at C, D and E respectively. If O is the origin, then the area (in sq. units) of the figure OCEB is equal to
View SolutionThe line 3x+2y=24 meets x - axis at B and the y -axis at A. The perpendicular bisector of AB meets the line through (0, -1) parallel to x -axis at C, then the area of the triangle ABC is_____
View SolutionThe area enclosed by 2|x|+3|y|≤6 is (a)3 sq. units (b) 4 sq. units (c)12 sq. units (d) 24 sq. units
View SolutionIf one side of a rhombus has endpoints (4, 5) and (1, 1), then the maximum area of the rhombus is 50 sq. units (b) 25 sq. units 30 sq. units (d) 20 sq. units
View SolutionThe area bounded by the curve y=4x−x2 and x-axis is (A) 307 sq. units (B) 317 sq. units (C) 323 sq. units (D) 343 sq. units
View SolutionOne diagonal of a square is 3x−4y+8=0 and one vertex is (-1, 1). The area of square is (a) 150 sq. unit (b) 125 sq. unit (c) 350 sq. unit (d) 225 sq. unit
View SolutionThe area of the triangle formed by the points P(0,1),Q(0,5)andR(3,4) is (a) 16 sq. units (b) 8 sq. units (c) 4 sq. units (d) 6 sq. units
View Solution