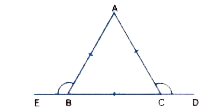
In the given figure ΔABC is equilateral on side AB produced. We choose a point such that A lies between P and B. We now denote 'a' as the length of sides of ΔABC, r1 as the radius of incircle ΔPAC and r2 as the ex-radius of ΔPBC with respect to side BC. Then r1+r2 is equal to
12
32a
√32a
a√2
The correct Answer is:C
From the given information, we get the following figure

∠CAP=120∘
So, in ΔPAC, using cosine rule, we get
PC2 a2+a2−2(a)2(−12)=3a2
In ΔPAC,
Perimeter =s1=2a+√3a2
Using formula for in radius, A2, we get
r1=√3a2×tan15∘=√3a2×(2−√3)
In ΔPBC, let r2 be exradius
Perimeter, s2=2a+a+√3a2
r=√3a2(1+√3)tan15∘(using r1=stan.A2)
=√3a2(1+√3)(2−√3)
∴r1+r2=√3a2(2−√3)(1+√3+1)=√3a2
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise (Multiple)
24 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise (Comprehension)
34 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise 5.11
4 Videos
- PROGRESSION AND SERIESBOOK - CENGAGECHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )
1 Videos
- PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEBOOK - CENGAGECHAPTER - PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEEXERCISE - Question Bank
15 Videos
Similar Questions
In the given figure ΔABC is equilateral on side AB produced. We choose a point such that A lies between P and B. We now denote 'a' as the length of sides of ΔABC, r1 as the radius of incircle ΔPAC and r2 as the ex-radius of ΔPBC with respect to side BC. Then r1+r2 is equal to
View SolutionIn the given figure, ΔABC is an equilateral triangle whose side BC has been produced in both the directions to D and E respectively. Prove that ∠ACD=∠ABE.
View Solution
Knowledge Check
The incircle of ΔABC touches side BC at D. The difference between BD and CD (R is circumradius of ΔABC) is
A∣∣∣4Rsin.A2sin.B−C2∣∣∣B∣∣∣4Rcos.A2sin.B−C2∣∣∣C|b−c|D∣∣∣b−c2∣∣∣
If ΔABC is a equilateral triangle and P, Q, R are mid-points of sides AB, BC and CA respectively then-
View SolutionThe incircle of ΔABC touches side BC at D. The difference between BD and CD (R is circumradius of ΔABC) is
View SolutionIn the given figure ABCD is a trapezium, P is the mid-point of side AD and PR||AB||DC.
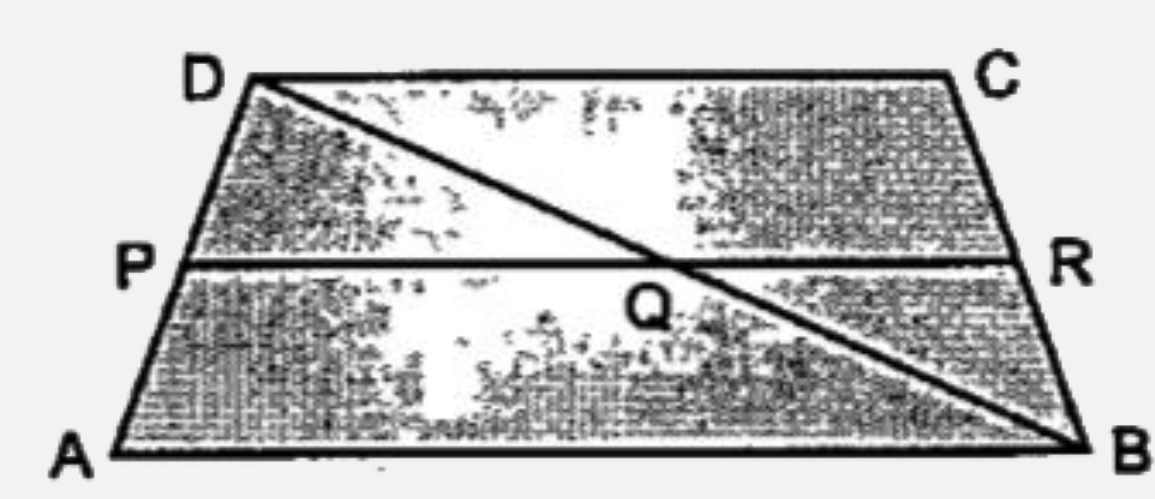
Prove that R is the mid-point of side BC
View SolutionLet the centroid of an equilateral triangle ABC be at the origin. Let one of the sides of equilateral triangle be along the straight line x+y=3. If R and r be the radius of circumcircle and incircle respectively of △ABC, then (R+r) is equal to :
View SolutionLet ABC be an equilateral triangle with side length a. Let R and r denote the radii of the circumcircle and the incircle of triangle ABC respectively. Then, as a function of a, the ratio Rr
View Solution
If a circle touches the side BC at point P, extended side AB at Q and extended side AC at R. Then AQ is equal to :
View SolutionIn ΔABC ,with usual notations r1,r2,r3 are in harmonic progression. If area of ΔABC is 24 and perimeter is 24 then length of its sides are
View Solution
