Let i=√−1 Define a sequence of complex number by z1=0,zn+1=(zn)2+i for n≥1. In the complex plane, how far from the origin is z111?Solution in Tamil
1
2
3
4
The correct Answer is:B
(b) z1=0, zn+1=z2n+i
Put n=1⇒z2=z21+i=i
Put n=2⇒z3=z22+i=i2+i=i−1
Put n=3⇒z4=z23+i=(i−1)2+i=−i
Put n=4⇒z5=z24+i=(−i)2+i=i−1
Put n=5⇒z6=z25+i=(i−1)2+i=−i
Thus z111=−1+i
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Multiple Correct Answer11videos
COMPLEX NUMBERS
- BOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Matching Column1videos
COMPLEX NUMBERS
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank16videos
CIRCLES
- BOOK - CENGAGECHAPTER - CONIC SECTIONSEXERCISE - Solved Examples And Exercises87videos
CONIC SECTIONS
Similar Questions
Complex numbers whose real and imaginary parts x and y are integers and satisfy the equation 3x2−|xy|−2y2+7=0
07:00View Solutionz1, z2, z3 are vertices of a triangle. Match the condition in List I with type of triangle in List II.
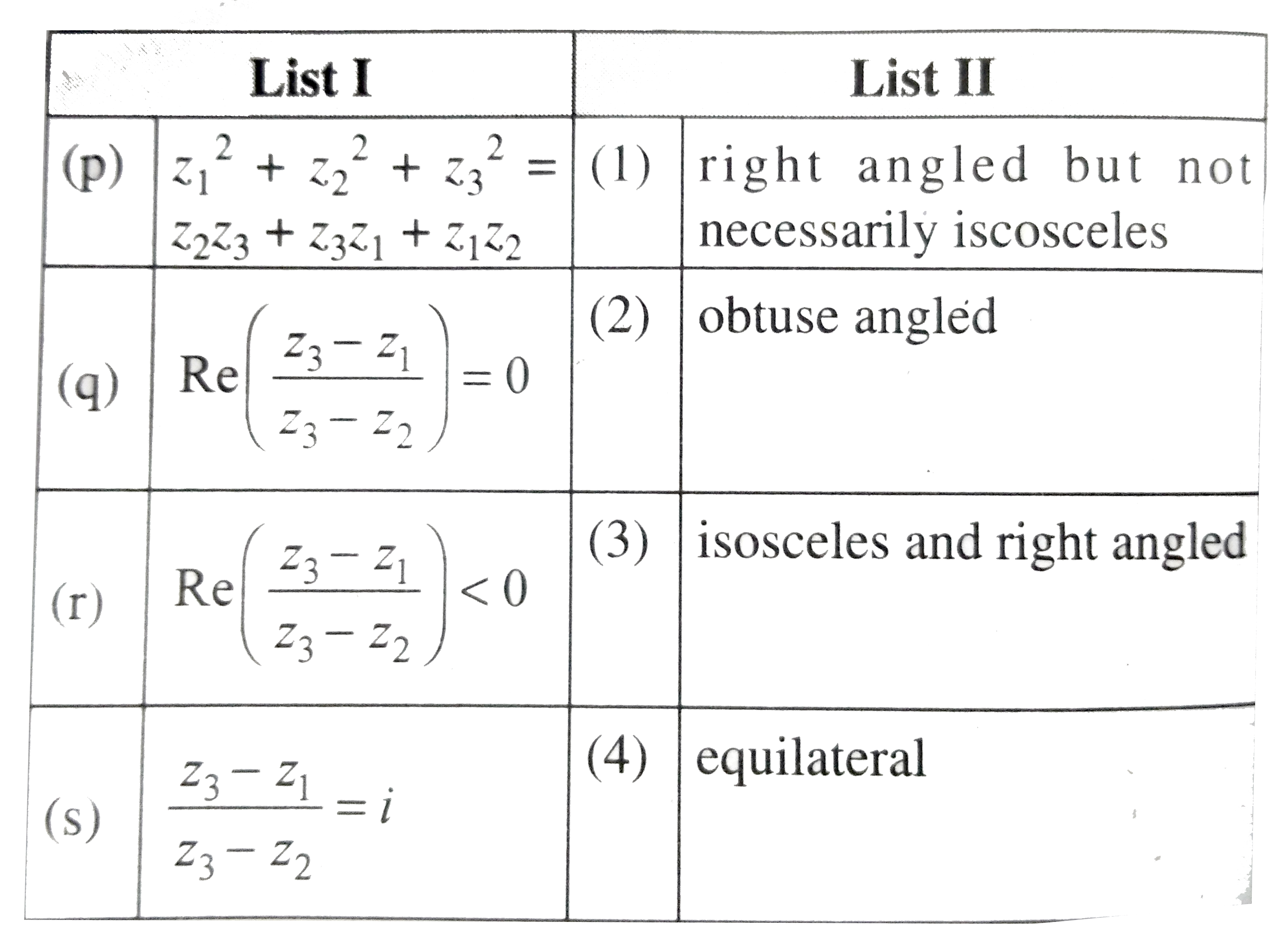
Codes05:55View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
View SolutionGiven that A(1,1) and B(2,−3) are two points and D is a point on AB produced such that AD=3AB. Find the coordinates of D.
03:14View SolutionLet i=sqrt(-1) Define a sequence of complex number by z_(1)=0,z_(n+1)=(z_(n))^(2)+i for n>=1. In the complex plane,how far from the origin is z_(111)?
View SolutionThe points A,B and C represent the complex numbers z1,z2,(1−i)z1+iz2 respectively, on the complex plane (where, i=√−1). The △ABC, is
03:02View SolutionLet a sequence x1,x2,x3,… of complex numbers be defined by x1=0,xn+1=x2n−i for all n>1, where i2=−1. Find the distance of x2000 from x1997 in the complex plane.
05:20View SolutionLet z1,z2,…...zn be a sequence of complex numbers defined by z1=−1−iandzn+1=z2n−i for all n≥1, then |z2013| is equal to
03:57View SolutionIf z1,z2,……zn are complex numbers such that |z1|=|z2|=….=|zn|=1, then |z1+z2+…..+zn| is equal to
03:58View SolutionLet z1,z2,z3,zn be the complex numbers such that |z1|=|z2|=|zn|=1. If z=(n∑k=1zk)(n∑k=11zk) then proves that z is a real number
02:58View SolutionLet i=√−1 Define a sequence of complex number by z1=0,zn+1=(zn)2+i for n≥1. In the complex plane, how far from the origin is z111?
03:51View Solutionयदि सम्मिश्र संख्यायें z1,z2,..............zn एक इकाई वृत |z| = 1 पर स्थित है तो सिद्ध कीजिये
|z1+z2+.............+zn|=∣∣z−11+z−12+................+z−1n∣∣05:10View SolutionThe points A,B and C represent the complex numbers z1,z2,(1−i)z1+iz2 respectively, on the complex plane (where, i=√−1). The △ABC, is
04:09View SolutionLet a sequence x1,x2,x3,… of complex numbers be defined by x1=0,xn+1=x2n−i for all n>1, where i2=−1. Find the distance of x2000 from x1997 in the complex plane.
04:26View SolutionIf z1,z2,z3………..zn are n complex numbers s.t, |z1|=|z2|=………….|zn|=1 then show that |z1+z2+…….+zn|=∣∣∣(1z1)+(1z2)+…..+(1zn)∣∣∣
02:57View Solution

