If a, b are complex numbers and one of the roots of the equation x2+ax+b=0 is purely real whereas the other is purely imaginery, and a2−¯a2=kb, then k isSolution in Tamil
2
4
6
8
The correct Answer is:B
(b) Let us consider α as the real and iβ as the imaginergy root. Then
α+iβ=−a
⇒α−iβ=−¯a
⇒2α=−(a+¯a) and 2iβ=−(a−¯a)
⇒4iαβ=a2−¯a2
⇒a2−¯a2=4b
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Multiple Correct Answer11videos
COMPLEX NUMBERS
- BOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Matching Column1videos
COMPLEX NUMBERS
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank16videos
CIRCLES
- BOOK - CENGAGECHAPTER - CONIC SECTIONSEXERCISE - Solved Examples And Exercises87videos
CONIC SECTIONS
Similar Questions
Complex numbers whose real and imaginary parts x and y are integers and satisfy the equation 3x2−|xy|−2y2+7=0
03:39View Solutionz1, z2, z3 are vertices of a triangle. Match the condition in List I with type of triangle in List II.
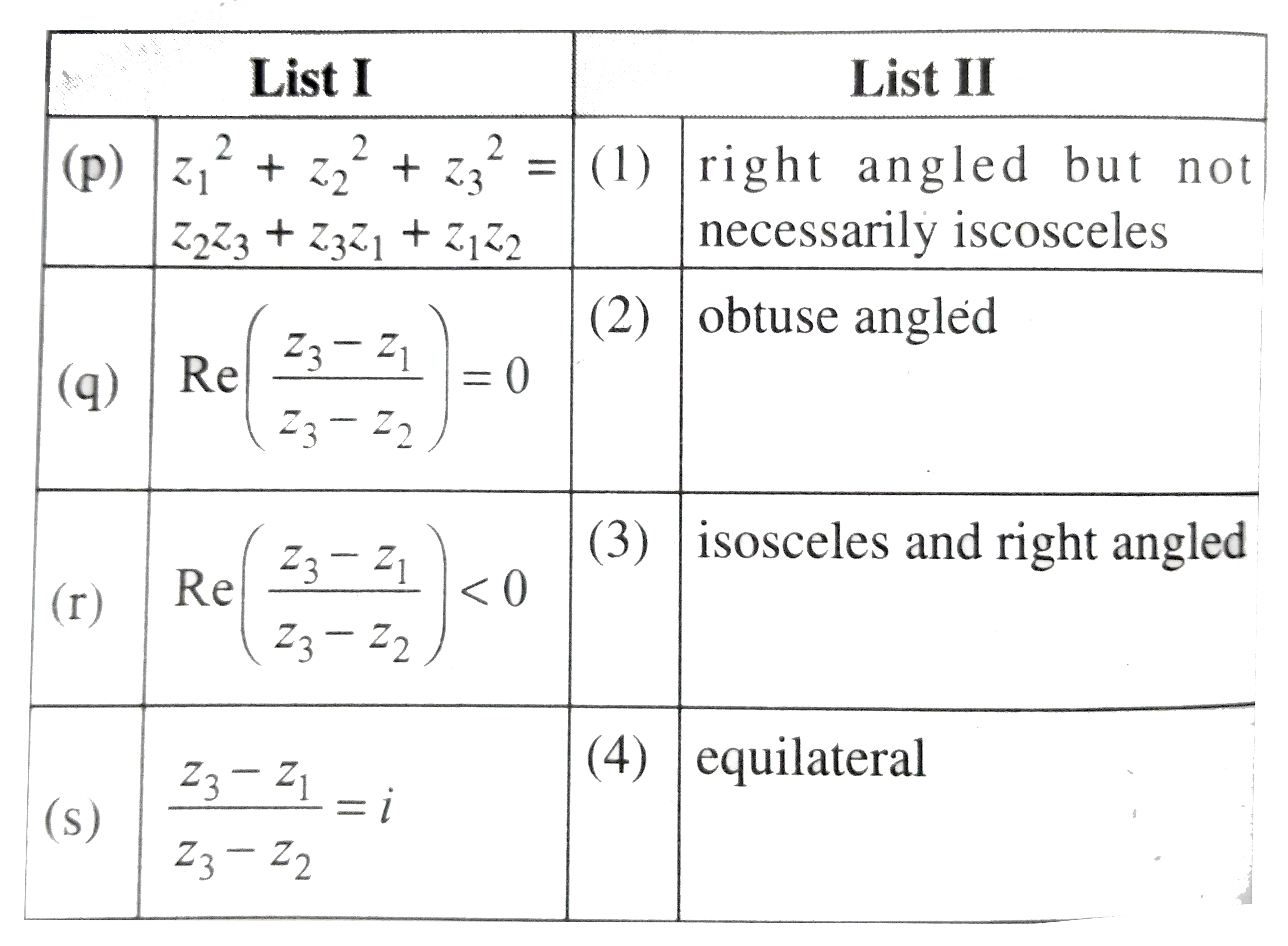
Codes02:22View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
03:05View SolutionGiven that A(1,1) and B(2,−3) are two points and D is a point on AB produced such that AD=3AB. Find the coordinates of D.
02:15View SolutionConsider the equation 10z2−3iz−k=0,wherez is a following complex variable and i2=−1. Which of the following statements ils true? For real complex numbers k , both roots are purely imaginary. For all complex numbers k , neither both roots is real. For all purely imaginary numbers k , both roots are real and irrational. For real negative numbers k , both roots are purely imaginary.
06:13View SolutionIf a,b are complex numbers and one of the roots of the equation x2+ax+b=0 is purely real, whereas the other is purely imaginary, prove that a2−a−2=4b.
02:30View SolutionIf a, b are complex numbers and one of the roots of the equation x2+ax+b=0 is purely real whereas the other is purely imaginery, and a2−¯a2=kb, then k is
02:44View SolutionIf a and b are complex and one of the roots of the equation x2+ax+b=0 is purely real whereas the other is purely imaginary, then
04:33View Solutionएक वर्ग समीकरण az2+bz+c=0 है, जहाँ a,b,c सम्मिश्र संख्यायें है।
समीकरण का एक पूर्णतः शुद्ध वास्तविक मूल होने की शर्त है03:03View SolutionConsider the equation 10z2−3iz−k=0,wherez is a following complex variable and i2=−1. Which of the following statements ils true? (a)For real complex numbers k , both roots are purely imaginary. (b)For all complex numbers k , neither both roots is real. (c)For all purely imaginary numbers k , both roots are real and irrational. (d)For real negative numbers k , both roots are purely imaginary.
View SolutionIf a,b are complex numbers and one of the roots of the equation x2+ax+b=0 is purely real, whereas the other is purely imaginary, prove that a2−(¯a)2=4b.
View SolutionIf a, b are complex numbers and one of the roots of the equation x2+ax+b=0 is purely real whereas the other is purely imaginery, and a2−¯a2=kb, then k is
05:14View SolutionIf a and b are complex and one of the roots of the equation x2+ax+b=0 is purely real whereas the other is purely imaginary, then
03:16View Solutionयदि समीकरण x2+ax+b=0 के मूल वास्तविक और भिन्न है तथा समीकरण x2+a|x|+b=0 का केवल एक वास्तविक मूल है, तो
03:29View Solutionयदि समीकरण x2+ax+b=0 के मूल वास्तविक और भिन्न है तथा समीकरण x2+a|x|b=0 का केवल एक वास्तविक मूल है, तो
03:31View Solution

