If the argument of (z−a)(¯z−b) is equal to that ((√3+i)1+√3i1+i) where a,b,c are two real number and z is the complex conjugate o the complex number z find the locus of z in the rgand diagram. Find the value of a and b so that locus becomes a circle having its centre at 12(3+i)Solution in Tamil
(3,2)
(2,1)
(2,3)
(2,4)
The correct Answer is:B
(b) (z−a)(¯z−b)=z¯z−a¯z−bz+ab⟨'z=x+iy)
Argument of (z−a)(¯z−b)=(y(a−b)x2+y2−ax+bx+ab)
Also, ((√3+i)1+√3i1+i=√3−√3+i(1+3)1+i=2+2i
Argument of 2+2i=tan−1(2/2)=π/4
⇒x2+y2−(a+b)x−(a−b)y+ab=0
Thus, the locus of z is a circle
Given centre is 3+i2
⇒a+b2=32 and a−b2=12
⇒a=2, b=1
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Multiple Correct Answer11videos
COMPLEX NUMBERS
- BOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Matching Column1videos
COMPLEX NUMBERS
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank16videos
CIRCLES
- BOOK - CENGAGECHAPTER - CONIC SECTIONSEXERCISE - Solved Examples And Exercises87videos
CONIC SECTIONS
Similar Questions
Complex numbers whose real and imaginary parts x and y are integers and satisfy the equation 3x2−|xy|−2y2+7=0
03:09View Solutionz1, z2, z3 are vertices of a triangle. Match the condition in List I with type of triangle in List II.
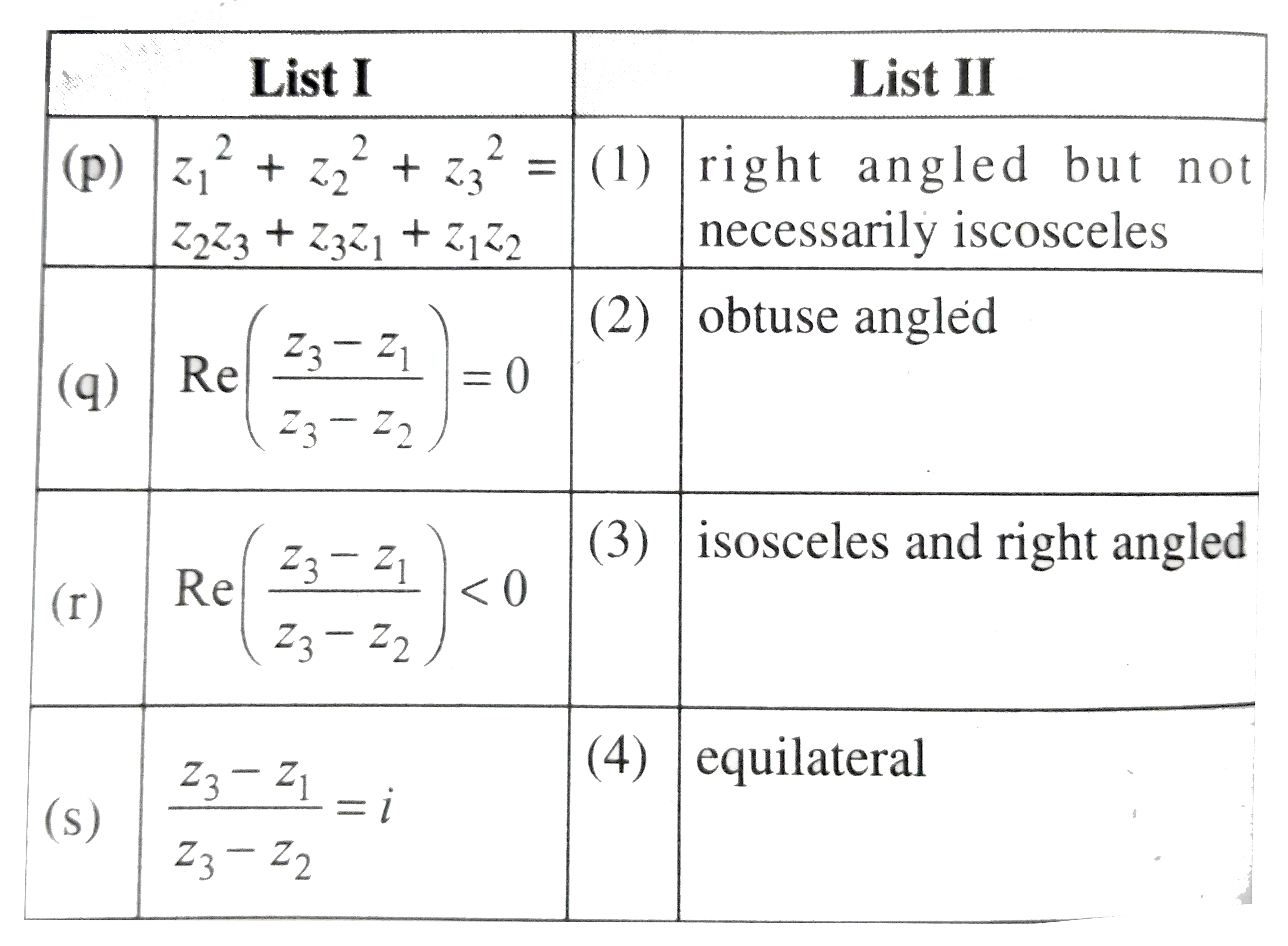
Codes05:28View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
03:43View SolutionGiven that A(1,1) and B(2,−3) are two points and D is a point on AB produced such that AD=3AB. Find the coordinates of D.
05:11View SolutionFind the modulus and the arguments of the complex number z=−1−i√3
03:30View SolutionIf complex number z lies on the curve |z-(-1+i)|=1, then find the locus of the complex number w=(z+i)/(1-i),i=sqrt(-1)1
01:13View SolutionFind the modulus and argument of the following complex number: z=−√3+i
04:02View SolutionIf the argument of (z−a)(¯z−b) is equal to that (√3+i)(1+√3i)1+i where a,b, are two real number and z is the complex conjugate of the complex number z find the locus of z in the Argand diagram. Find the value of a and b so that locus becomes a circle having its centre at 12(3+i)
05:28View SolutionLet z be a complex number such that |z| + z = 3 + i (Where i=√−1) Then ,|z| is equal to
03:05View SolutionIf the argument of (z−a)(¯z−b) is equal to that of (√3+i)(1+√3i)1+i , where a,b are two real numbers and ¯z is the complex conjugate of the Argand diagram. Find the values of a and b so that be locus becomes a circle having its centre at 12(3+i).
02:51View SolutionFor a complex number Z, if the argument of (Z−a)(¯¯¯Z−b) is π4 or −3π4 (where a, b are two real numbers), then the value of ab such that the locus of Z represents a circle with centre 32+i2 is (where, i2=−1)
03:12View SolutionIf |Z−i|=√2 then arg(Z−1Z+1) is (where i=√−1) ; Z is a complex number )
05:03View SolutionFind modulus and argument of the complex numbers
z=−√3+i03:50View SolutionFind modulus and argument of the complex numbers
z=−√3+i01:56View SolutionFind modulus and argument of the complex numbers
z=−√3+i03:34View SolutionIf the argument of (z−a)(¯z−b) is equal to that ((√3+i)1+√3i1+i) where a,b,c are two real number and z is the complex conjugate o the complex number z find the locus of z in the rgand diagram. Find the value of a and b so that locus becomes a circle having its centre at 12(3+i)
05:18View Solution

