If |z|=1 and z'=1+z2z, thenSolution in Tamil
z' lie on a line not passing through origin
|z'|=√2
Re(z')=0
Im(z')=0
The correct Answer is:D
(d) z'=1+z2z=z¯z+zz=z+¯z which is purely real.
⇒Im(z')=0
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Multiple Correct Answer11videos
COMPLEX NUMBERS
- BOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Matching Column1videos
COMPLEX NUMBERS
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank16videos
CIRCLES
- BOOK - CENGAGECHAPTER - CONIC SECTIONSEXERCISE - Solved Examples And Exercises87videos
CONIC SECTIONS
Similar Questions
Complex numbers whose real and imaginary parts x and y are integers and satisfy the equation 3x2−|xy|−2y2+7=0
04:49View Solutionz1, z2, z3 are vertices of a triangle. Match the condition in List I with type of triangle in List II.
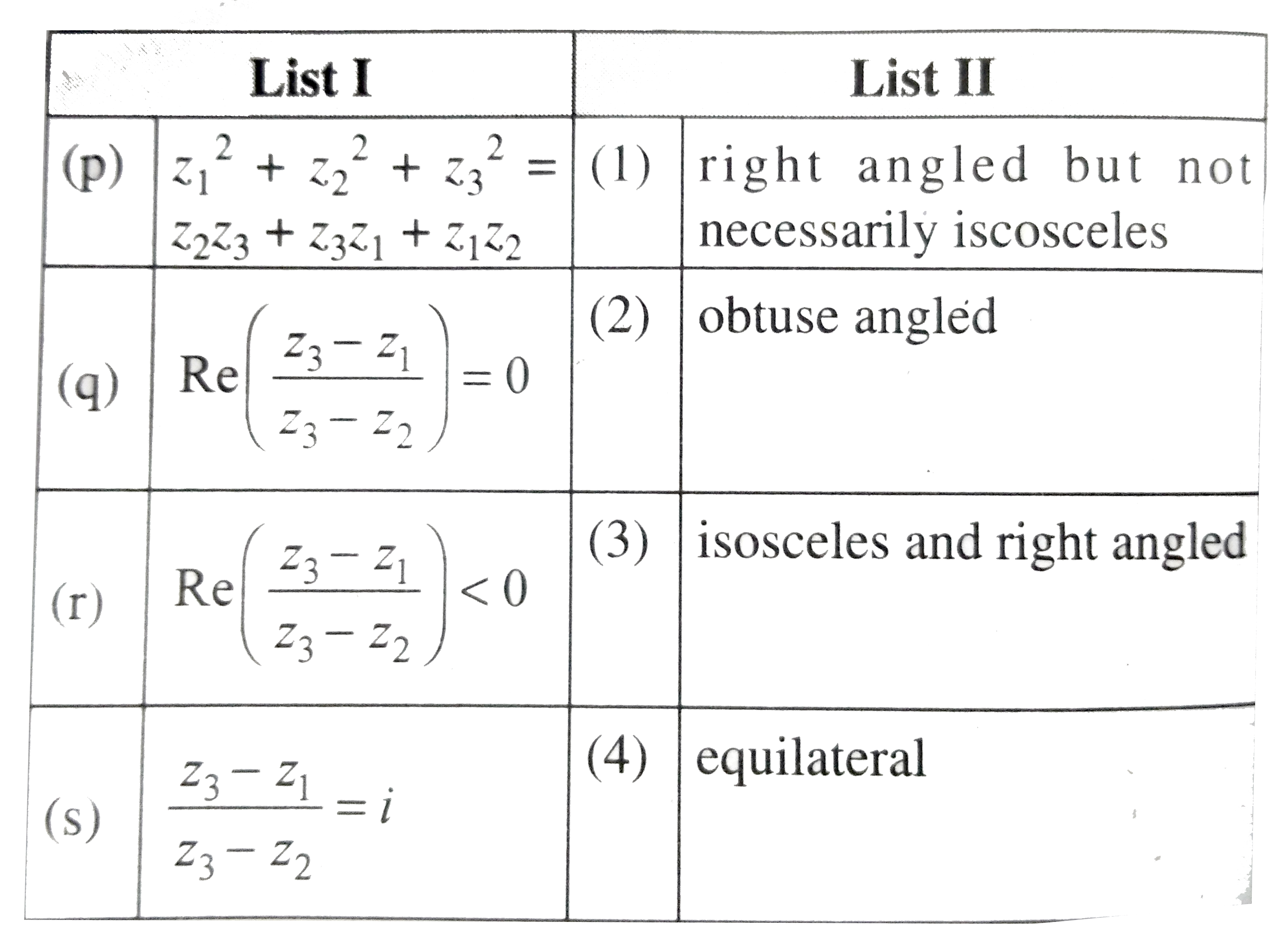
Codes01:14View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
03:42View SolutionGiven that A(1,1) and B(2,−3) are two points and D is a point on AB produced such that AD=3AB. Find the coordinates of D.
04:21View SolutionIf z^(2)+z+1=0 where z is a complex number, then the value of (z+(1)/(z))^(2)+(z^(2)+(1)/(z^(2)))^(2)+...+(z^(6)+(1)/(z^(6)))^(2) is
01:44View SolutionIf |z|=1 and z'=1+z2z, then
01:31View Solutionकिन्ही दो सम्मिश्र संख्याएँ z1 तथा z2 के लिए साबित कीजिये कि
|z1+z2|2+|z1−z2|2=2[|z1|2+|z2|2]06:00View Solutionयदि (If)|z1|=|z2|=1 तो साबित कीजिये कि
|z1+z2|=∣∣∣1z1+1z2∣∣∣04:49View Solutionयदि [If]z1=2−i,z2=1+i, ज्ञात कीजिये ∣∣∣z1+z2+1z1−z2+i∣∣∣
05:26View SolutionIf |z|=1 and z'=1+z2z, then
03:44View Solutionयदि z1 तथा z2 दो सम्मिश्र संख्याएँ हैं तथा z1z2+z2z1=1, तब
03:39View SolutionIf z^2+z+1=0 where z is a complex number, then the value of (z+1/z)^2+(z^2+1/z^2)^2+....+(z^6+1/z^6)^2 is
02:55View Solutionif z2+z+1=0, then the value of (z+1z)2+(z2+1z2)2+(z3+1z3)2+......+(z21+1z21)2 is
03:50View SolutionIf (z)1=2−i, (z)2=1+i, find ∣∣∣(z)1+(z)2+1(z)1−(z)2+1∣∣∣
05:03View SolutionIf 2z13z2 is a purely imaginary, then ∣∣∣z1−z2z1+z2∣∣∣ is:
01:45View Solution

