If ω is any complex number such that zω=|z|2 and |z−¯z|+|ω+¯¯ω|=4, then as ω varies, then the area bounded by the locus of z isSolution in Tamil
4 sq. units
8 sq. units
16 sq. units
12 sq. units
The correct Answer is:B
(b) zω=|z|2
⇒zω=z¯z
⇒ω=¯z
∴|z−¯z|+|z+¯z|=4
∴|x|+|y|=2
which is a square ∴ Area =8sq. units
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Multiple Correct Answer11videos
COMPLEX NUMBERS
- BOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Matching Column1videos
COMPLEX NUMBERS
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank16videos
CIRCLES
- BOOK - CENGAGECHAPTER - CONIC SECTIONSEXERCISE - Solved Examples And Exercises87videos
CONIC SECTIONS
Similar Questions
Complex numbers whose real and imaginary parts x and y are integers and satisfy the equation 3x2−|xy|−2y2+7=0
09:41View Solutionz1, z2, z3 are vertices of a triangle. Match the condition in List I with type of triangle in List II.
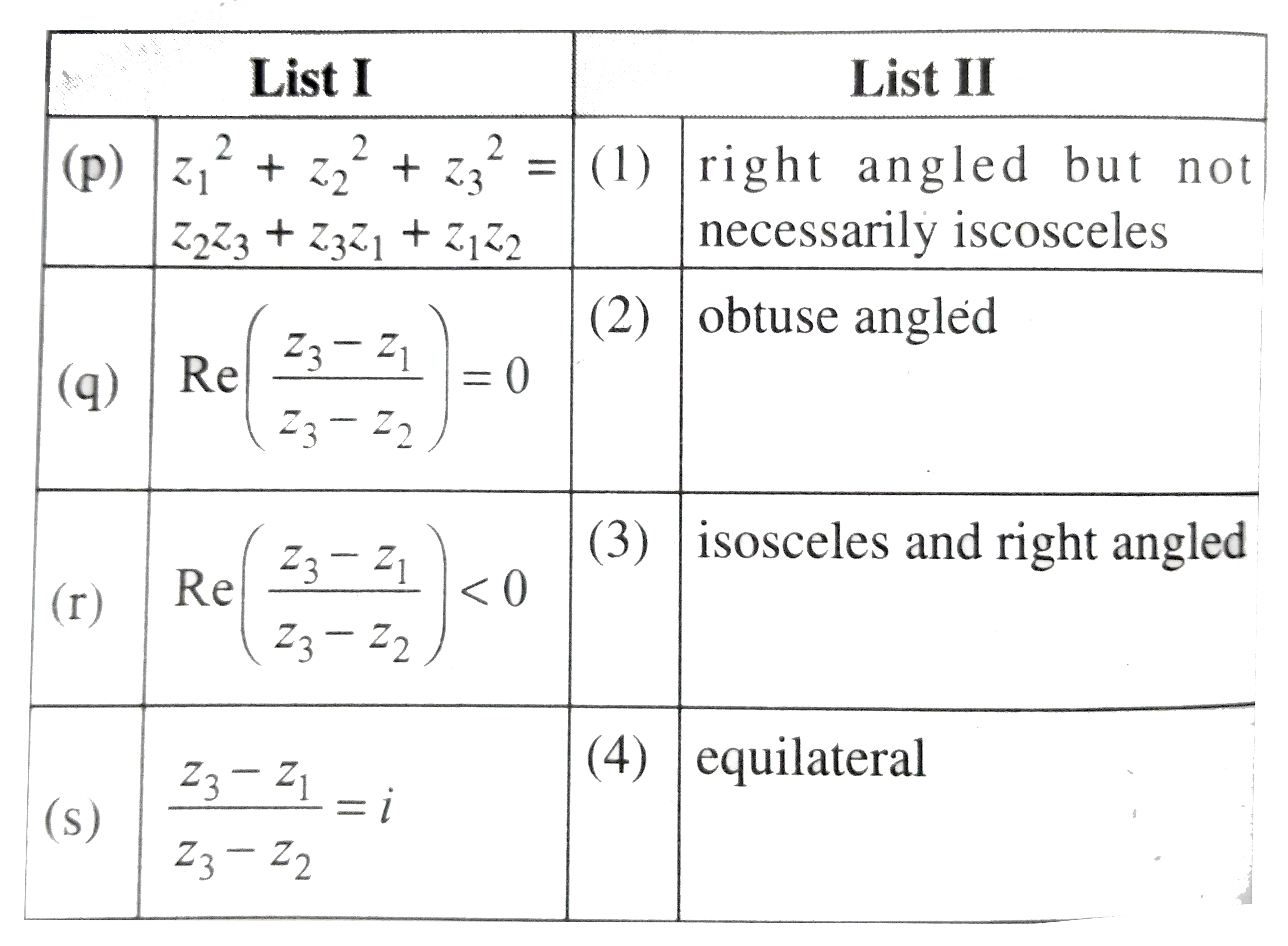
Codes05:48View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
01:54View SolutionGiven that A(1,1) and B(2,−3) are two points and D is a point on AB produced such that AD=3AB. Find the coordinates of D.
03:07View SolutionFor complex numbers z and w, prove that |z|^(2)w-|w|^(2)z=z-w, if and only if z=w or zbar(w)=1.
02:55View SolutionIf omega is any complex number such that z omega = |z|^2 and |z - barz| + |omega + bar(omega)| = 4 then as omega varies, then the area bounded by the locus of z is
03:38View SolutionLet z and omega be two non zero complex numbers such that |z|=|omega| and argz+argomega=pi, then z equals (A) omega (B) -omega (C) baromega (D) -baromega
02:37View SolutionIf ω is any complex number such that zω=|z|2 and |z−¯z|+|ω+¯¯ω|=4, then as ω varies, then the area bounded by the locus of z is
06:58View SolutionLet z and omega be complex numbers such that |z|=|ω| and arg (z) dentoe the principal of z.
Statement-1: If argz+ arg ω=π, then z=−¯¯ω
Statement -2: |z|=|ω| implies arg z-arg ¯¯ω=π, then z=−¯¯ω03:49View SolutionLet z and w be non - zero complex numbers such that zw=∣∣z2∣∣ and |z−¯z|+|w+¯¯¯w|=4. If w varies, then the perimeter of the locus of z is
View Solutionसम्मिश्र संख्याओं z तथा ω के लिए सिद्ध कीजिए कि |z|2ω−|ω|2z=z−ω होगा यदि z=ω या z¯¯ω=1 हो।
04:27View SolutionIf ω is any complex number such that zω=|z|2 and |z−¯z|+|ω+¯¯ω|=4, then as ω varies, then the area bounded by the locus of z is
03:25View SolutionLet z, ω be complex numbers such that ¯z+i¯¯ω=0 and arg(zω)=π, then argz equals
02:27View SolutionIf ω is any complex number such that zω=|z|2 and |z−¯z|+|ω+¯¯ω|=4, then as ω varies, then the area of locus of z is
04:10View SolutionLet z and omega be complex numbers such that |z|=|ω| and arg (z) dentoe the principal of z.
Statement-1: If argz+ arg ω=π, then z=−¯¯ω
Statement -2: |z|=|ω| implies arg z-arg ¯¯ω=π, then z=−¯¯ω01:42View Solution

