Let z1andz2q, be two complex numbers with αandβ as their principal arguments such that α+β then principal arg(z1z2) is given by:Solution in Tamil
α+β+π
α+β−π
α+β−2π
α+β
The correct Answer is:C
(c) arg(z1z2)=arg(z1)+arg(z2)+2mπ, m∈I
∴ Principal argument =α+β−2π
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Multiple Correct Answer11videos
COMPLEX NUMBERS
- BOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Matching Column1videos
COMPLEX NUMBERS
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank16videos
CIRCLES
- BOOK - CENGAGECHAPTER - CONIC SECTIONSEXERCISE - Solved Examples And Exercises87videos
CONIC SECTIONS
Similar Questions
Complex numbers whose real and imaginary parts x and y are integers and satisfy the equation 3x2−|xy|−2y2+7=0
03:22View Solutionz1, z2, z3 are vertices of a triangle. Match the condition in List I with type of triangle in List II.
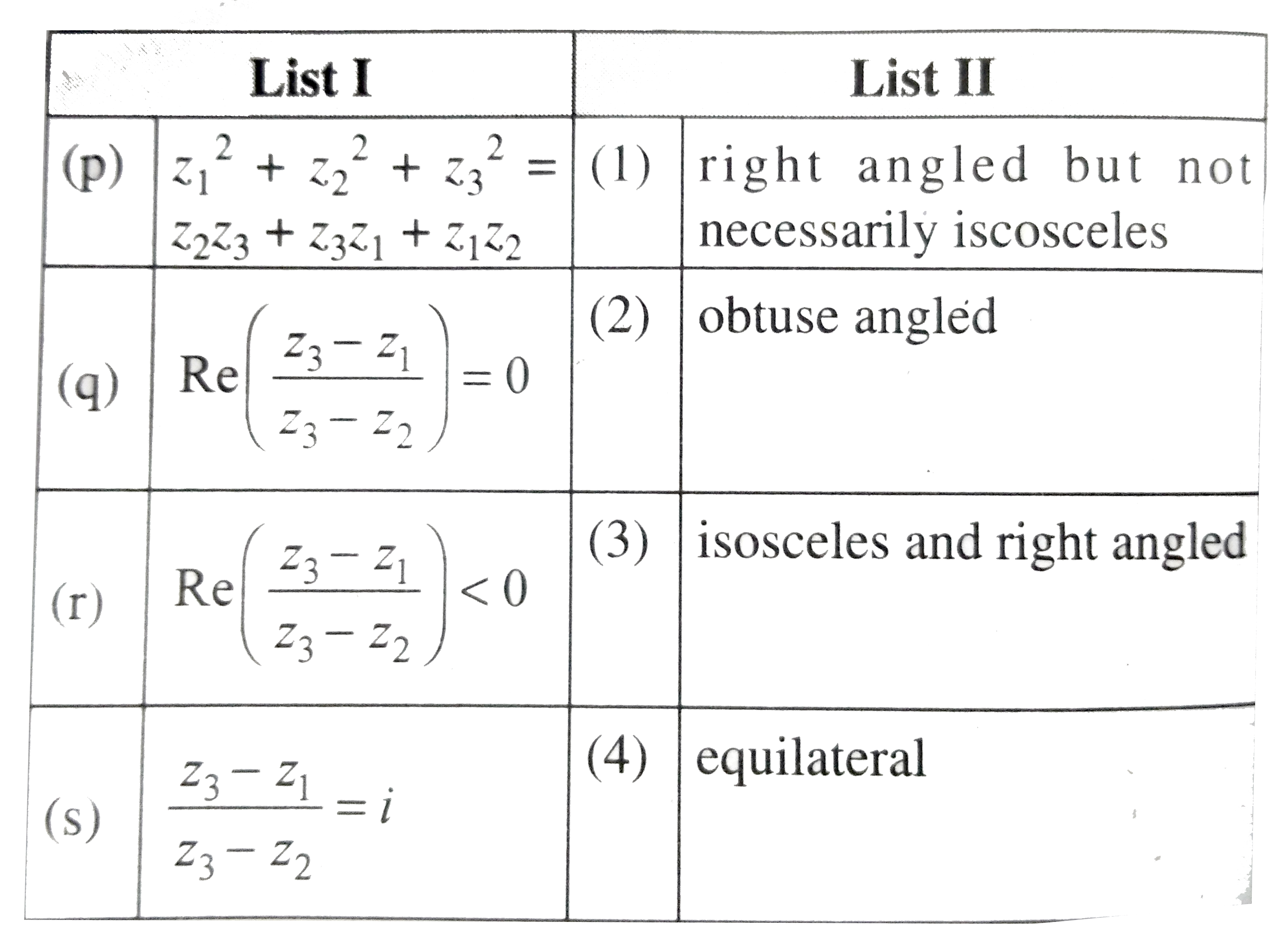
Codes03:50View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
03:13View SolutionGiven that A(1,1) and B(2,−3) are two points and D is a point on AB produced such that AD=3AB. Find the coordinates of D.
View SolutionLet z_(1) and z_(2)q ,be two complex numbers with alpha and beta as their principal arguments suith that alpha+beta then principal arguments suiven by:
View SolutionWhich of the following are correct for any two complex numbers z1andz2? (A) |z1z2|=|z1||z2| (B) arg(|z1z2|)=(argz1)(arg,z2) (C) |z1+z2|=|z1|+|z2| (D) |z1−z2|≥|z1|−|z2|
04:27View SolutionA : If argument of z1=π/3 , argument of z2=π/4 then argument of z1z2 is 7π/12
R : Arg (z1z2)=Argz1+Argz203:29View SolutionIf arg (Z_1) =170° and arg(Z_2) =70° find the principal argument of Z_1 Z_2
03:38View SolutionIf arg (Z_1) =170° and arg(Z_2) =70° find the principal argument of Z_1 Z_2
02:01View Solutionনীচের প্রত্যেকটি জটিল সংখ্যার আর্গুমেন্টের মান নির্ণয় করো: z1=√3+i,z2=−1−i√3 এরপর, arg(z1z2) ও arg(z1z2) -এর মান নির্ণয় করো।
03:30View SolutionIf z_1 And z_2 If there are two complex numbers Re(z_1z_2) =
04:06View Solutionयदि z1,z2 दो सम्मिश्र संख्याएँ इस प्रकार हैं कि z1+z2 तथा z1z2 दोनों वास्तविक हैं तब
03:37View Solutionमाना z1 व z2 दो सम्मिश्र संख्यायें हैं जिनके मुख्य कोणांक α व β इस प्रकार हैं कि α+β>π, तो (z1z2) का मुख्य कोणांक होगा
04:04View SolutionIf |2z−1|=|z−2|andz1,z2,z3 are complex numbers such that |z1−α|<α,|z2−β|<β, then= ∣∣∣z1+z2α+β∣∣∣a)<|z|b. <2|z|c.>|z| d. >2|z|
03:17View SolutionLet z1andz2q, be two complex numbers with αandβ as their principal arguments such that α+β then principal arg(z1z2) is given by:
04:18View Solution

