Let arg(zk)=(2k+1)πn where k=1,2,………n. If arg(z1,z2,z3,………….zn)=π, then n must be of form (m∈z)Solution in Tamil
4m
2m−1
2m
None of these
The correct Answer is:B
(b) arg(z1,z2,z3……….zn)=π
⇒arg(z1)+arg(z2)+….+arg(zn)=π±2mπ, m∈I
⇒πn[3+5+7+….+(2n+1)]=π±2mπ
⇒πn[n2[6+2(n−1)]]=π±2mπ
⇒3+n−1=1±2m
⇒n=−1=1±2m
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Multiple Correct Answer11videos
COMPLEX NUMBERS
- BOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Matching Column1videos
COMPLEX NUMBERS
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank16videos
CIRCLES
- BOOK - CENGAGECHAPTER - CONIC SECTIONSEXERCISE - Solved Examples And Exercises87videos
CONIC SECTIONS
Similar Questions
Complex numbers whose real and imaginary parts x and y are integers and satisfy the equation 3x2−|xy|−2y2+7=0
04:32View Solutionz1, z2, z3 are vertices of a triangle. Match the condition in List I with type of triangle in List II.
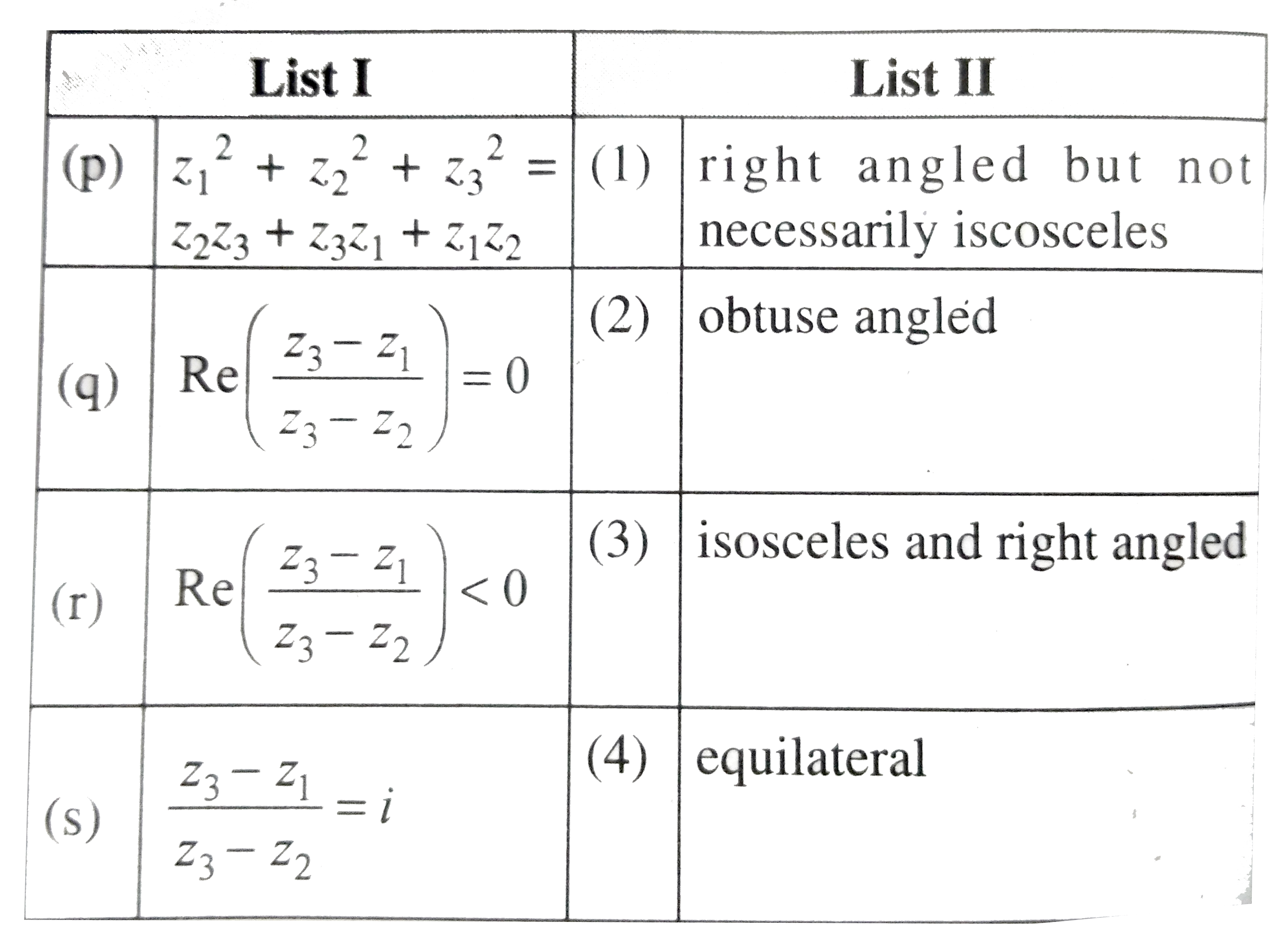
Codes08:17View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
03:50View SolutionGiven that A(1,1) and B(2,−3) are two points and D is a point on AB produced such that AD=3AB. Find the coordinates of D.
03:15View SolutionLet z1z2,z3zn be the complex numbers such that |z1|=|z2||zn|=1. If z=(n∑k=1zk)(n∑k=11zk) then proves that z is a real number 0<z≤n2
04:39View SolutionIf arg(Z_(1)Z_(2))=arg Z_(1)+arg Z_(2)+n pi,n in Z and ifprinciple argument of Z in[-pi,pi) then Z_(1)=-2,Z_(2)=-3 then n=
07:22View SolutionIf arg(z_(2)-z_(1))+arg(z_(3)-z_(1))=2arg(z-z_(1)) where z,z_(1),z_(2) and z_(3) ,are complex numbers, then the locus of z is
03:03View SolutionIf z_(1),z_(2).........z_(n)=z, then arg z_(1)+arg z_(2)+......+argz_(n) and arg z differ by a
02:01View SolutionLet | z_ (1) | = | z_ (2) | and arg (z_ (1)) + arg (z_ (2)) = (pi) / (2) then
02:38View SolutionLet z_(1),z_(2),z_(3) be complex numbers (not all real) such that |z_(1)|=|z_(2)|=|z_(3)|=1 and 2(z_(1)+z_(2)+z_(3))-3z_(1)z_(2)z_(3) is real.Then,Max(arg(z_(1)),arg(z_(2)),arg(z_(3))) (Given that argument of z_(1),z_(2),z_(3) is possitive ) has minimum value as (k pi)/(6) where (k+2) is
03:25View SolutionLet arg(zk)=(2k+1)πn where k=1,2,………n. If arg(z1,z2,z3,………….zn)=π, then n must be of form (m∈z)
05:04View SolutionIf z1,z2,z3,…………..,zn are n nth roots of unity, then for k=1,2,,………,n
05:53View SolutionIf zn=cosnπ3+isinnπ3,thenz1,z2….Z6 is
05:29View SolutionIf z=z1z2z3….....zn prove that argz−(argz1+argz2+….........+argzn)=2nπ1n∈I.
01:39View SolutionIf z1,z2andz3 are three distinct complex numbers such that |z1|=1,|z2|=2,|z3|=4,arg(z2)=arg(z1)−π,arg(z3)=arg(z1)+π/2, then z2z3 is equal to
02:10View Solution

