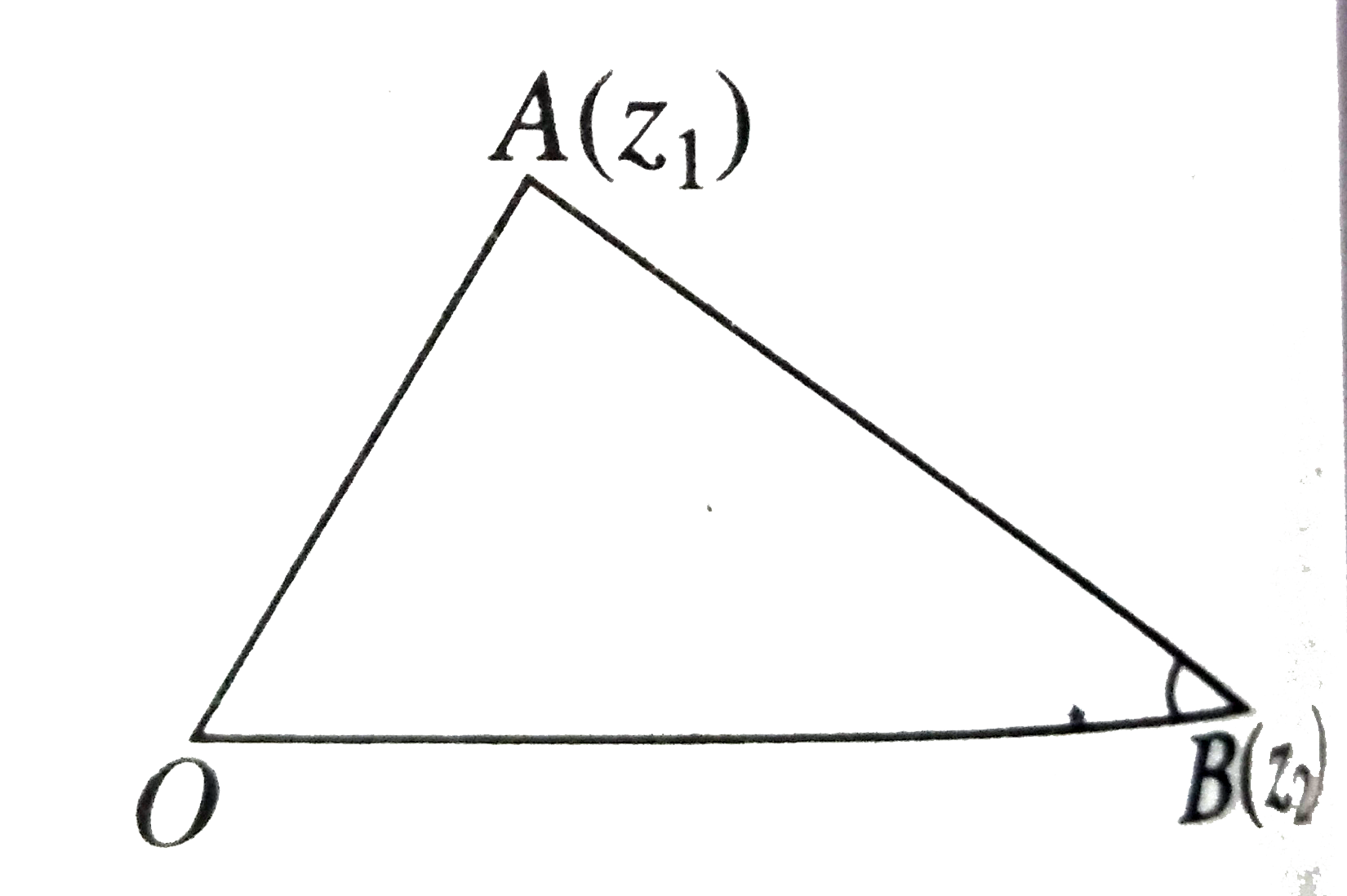
Let A(z1) and B(z2) are two distinct non-real complex numbers in the argand plane such that z1z2+¯z1z2=2. The value of |∠ABO| is
A
π6
B
π4
C
π2
D
None of these
Text Solution
The correct Answer is:C
(c) z1z2+¯z1¯z2=2
⇒Re(z1z2)=1
Let z1z2=x+iy⇒x=1
Now, arg(z1−z2−z2)=arg(1−z1z2)=arg(−iy)=±π2
∠ABO=π2
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Multiple Correct Answer11videos
COMPLEX NUMBERS
- BOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Matching Column1videos
COMPLEX NUMBERS
- BOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank16videos
CIRCLES
- BOOK - CENGAGECHAPTER - CONIC SECTIONSEXERCISE - Solved Examples And Exercises87videos
CONIC SECTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
For two complex numbersz1andz2 , we have ∣∣∣z1−z21−¯z1z2∣∣∣=1, then
Aboth z1andz2 lie on circle |z|=1Barg(z1z2)=π3CAt least one of z1andz2 lies on the circle |z|=1D|z1|=2|z2| - Question 2 - Select One
Let z1andz2 be two non-zero complex number such that |z1|=|z2|=∣∣ ∣∣1z1+1z2∣∣ ∣∣=2
What is the value of |z1+z2| ?A8B4C2D1 - Question 3 - Select One
If z1andz2 are two distinct non-zero complex number such that |z1|=|z2|, then z1+z2z1−z2 is always
Apurely realBpurely imaginaryCequal to zeroDNone of these
If z1 and z2 are two non-zero complex number such that |z1z2|=2 and arg(z1)−arg(z2)=π2 ,then the value of 3iz1z2
View SolutionIf z1 and z2 are two complex numbers such that ∣∣∣z1−z2z1+z2∣∣∣=1, then
View SolutionIf z1 and z2 are two complex numbers such that |z1|<1<|z2|, then prove that |(1−z1¯z2)/(z1−z2)|<1
View SolutionIf z1 and z2 are two complex numbers such that |z1|<1<|z2|, then prove that |(1−z1¯z2)/(z1−z2)|<1
View SolutionLet z1,z2 be two distinct complex numbers with non-zero real and imaginary parts such that arg(z1+z2)=π/2, then arg(z1+¯z1)−arg(z2+¯z2) is equal to
View Solution

