Consider the region $R$ in the Argand plane described by the complex number. $Z$ satisfying the inequalities $| Z - 2 | \leq | Z - 4 |$ , $| Z - 3 | \leq | Z + 3 |$ , $| Z - i | \leq | Z - 3 i |$ , $| Z + i | \leq | Z + 3 i |$
Answer the followin questions :
The maximum value of $| Z |$ for any $Z$ in $R$ is

A

$5$

B

$3$

C

$1$

D

$\sqrt{13}$

Text Solution

Verified by Experts

The correct Answer is:D

$(d)$ $| Z - 2 | \leq | Z - 4 | \Rightarrow {| Z - 2 |}^{2} \leq {| Z - 4 |}^{2}$
$\Rightarrow {(x - 2)}^{2} + y^{2} \leq {(x - 4)}^{2} + y^{2}$
$\Rightarrow 8 x - 4 x \leq 16 - 4$
$\Rightarrow x \leq 3$
$| Z - 3 | \leq | Z + 3 | \Rightarrow x \geq 0$
$| Z - i | \leq | Z - 3 i | \Rightarrow y \leq 2$
$| Z + i | \leq | Z + 3 i | \Rightarrow y \geq - 2$
So, $z$ lies on or inside rectangle formed by lines $x = 0$ , $x = 3$ , $y = - 2$ and $y = 2$ .
$(1)$ Max of $| Z | = O C$ or $O B = \sqrt{3^{2} + 2^{2}} = \sqrt{13}$

|

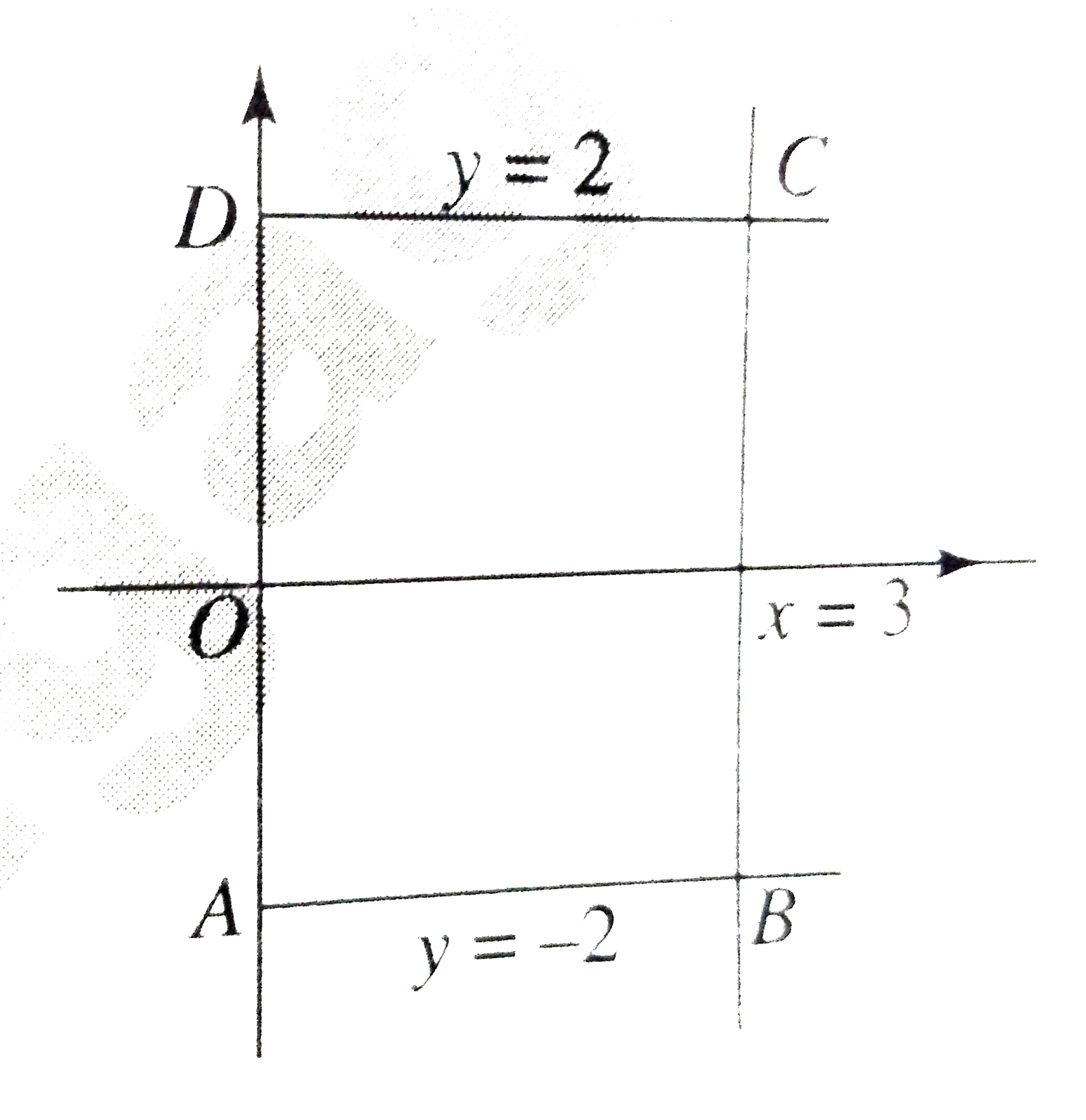
Updated on:21/07/2023

Class 12 MATHS COMPLEX NUMBERS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Consider the region $R$ in the Argand plane described by the complex number. $Z$ satisfying the inequalities $| Z - 2 | \leq | Z - 4 |$ , $| Z - 3 | \leq | Z + 3 |$ , $| Z - i | \leq | Z - 3 i |$ , $| Z + i | \leq | Z + 3 i |$
Answer the followin questions :
Minimum of $| Z_{1} - Z_{2} |$ given that $Z_{1}$ , $Z_{2}$ are any two complex numbers lying in the region $R$ is
A $0$
B $5$
C $\sqrt{13}$
D $3$
Question 2 - Select One
The complex number z satisfying $| z - 1 | = | z - 3 | = | z - i |$ is
A2 +i
B $\frac{3}{2} + \frac{1}{2} i$
C $2 + 2 i$
Dnone of these
Question 3 - Select One
IF $| z + 4 | \leq 3,$ then the maximum value of $| z + 1 |$ is
A0
B4
C6
D10

CENGAGE-COMPLEX NUMBERS-Comprehension

Home
Ask Doubt
Profile