Question

Find the values of x for which the following functions are identical.
(i) $f\left(x\right)=x\text{and}g\left(x\right)=\frac{1}{1/x}$
(ii) $f\left(x\right)=\frac{\sqrt{9-x^2}}{\sqrt{x-2}}\text{and}g\left(x\right)=\sqrt{\frac{9-x^2}{x-2}}$

Explanation

(i) `f(x) = x` is defined for all x.
but `g(x) = (1)/(1//x) =x` is not defined for `x=0` as `1//x` is not defined at `x=0`.
Hence both the functions are identical for ` x in R - {0}.`
(ii) `f(x)=(sqrt(9-x^(2)))/(sqrt(x-2))` is defined if ` 9-x^(2) ge 0 " and " x-2 gt 0`
`implies x in [-3,3] " and " x gt 2 implies x in (2, 3]`
` g(x) =sqrt((9-x^(2))/(x-2))` is defined if `(9-x^(2))/(x-2) ge 0`
`implies (x^(2)-9)/(x-2) le 0`

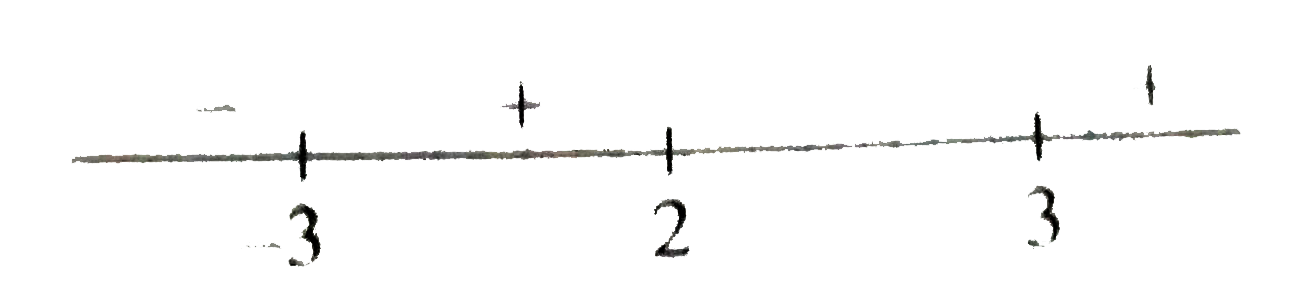
From the sign scheme `x in (-oo, -3] cup (2,3]`
Hence, f(x) and g(x) are identical if `x in (2,3]`