Consider the function f(x)={x−[x]−12,ifx∉Io,ifx∈I,where[.] denotes the fractional integral function and I is the set of integers. Then find g(x)=max.x2,f(x),|x|;−2≤x≤2.Solution in Tamil
Clearly, from graph,
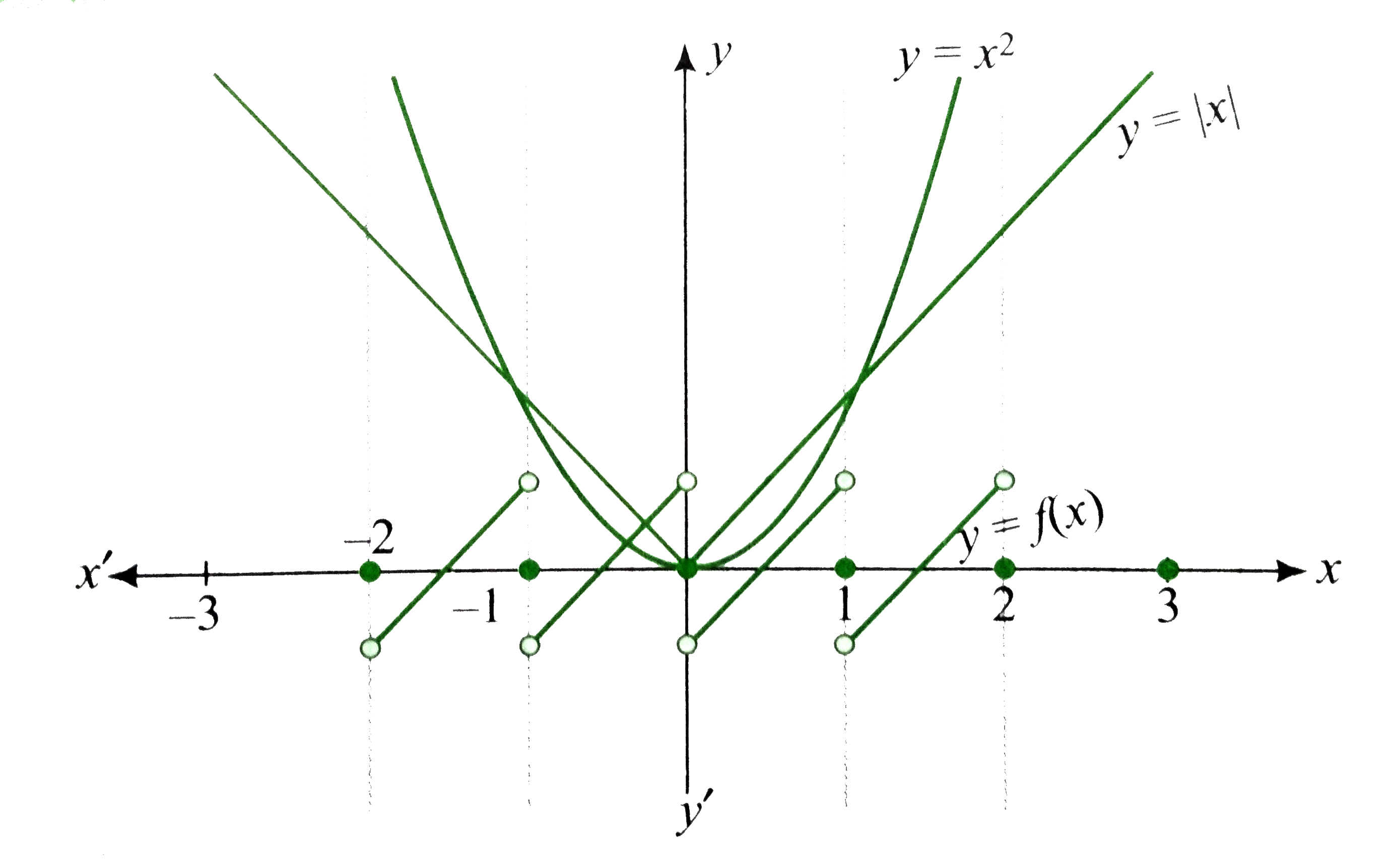
g(x)=⎧⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪⎩x2,−2≤x≤−1−x,−1<x≤−1/412+x,−14<x<0x,0≤x<1x2,1≤x<2
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise 1.115videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise 1.25videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - JEE Previous Year12videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGECHAPTER - Quadratic Equations, Inequalities, Modulus and LogarithmsEXERCISE - Question Bank28videos
Quadratic Equations, Inequalities, Modulus and Logarithms
- BOOK - CENGAGECHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.311videos
SCALER TRIPLE PRODUCTS
Similar Questions
If sets A=[−4,1]andB=[0,3), then find the following sets:
(a) A∩B (b) A∪B (c ) A−B
(d) B−A (e ) (A∪B)' (f) (A∩B)'01:46View Solution(a) If n(A)=6 and n(A×B)=42 then find n(B)
(b) If some of the elements of A×B are (x,p),(p,q),(r,s). Then find the minimum value of n(A×B).05:26View SolutionFor real x, let f(x)=x3+5x+1 , then (1) f is oneone but not onto R (2) f is onto R but not oneone (3) f is oneone and onto R (4) f is neither oneone nor onto R
05:43View SolutionLet a,b,c,d be positive integers such that (log)ab=32and(log)cd=54. If (a−c)=9, then find the value of (b−d).
02:46View SolutionNumber of integral value(s) of λ for which vectors x2ˆi−ˆj+xˆk,(λ−1)ˆi−2λˆj+ˆk and ˆi−ˆj+ˆk, in the order from right-handed system ∀x ∈R, is
03:23View SolutionLet A={x∈R:0≤x≤1}. If f:A→A is defined by f(x)={x,ifxQ1−x,ifxQ then prove that fof(x)=x for all x∈A.
05:27View SolutionIf f(x0=x+{−x}+[x], where [x] is the integral part& {x} is the fractional part of x. Discuss the continuity of f in [−2, 2] .
05:00View SolutionConsider the function f(x)={x−[x]−12x∉0x∈I where [.] denotes the fractional integral function and I is the set of integers. Then find g(x)max.[x2,f(x),|x|},−2≤x≤2.
04:45View SolutionFind the points of discontinuity of the function: f(x)=[[x]]−[x−1],where[.] represents the greatest integer function
01:50View SolutionDiscuss the differentiability of f(x)=[x]+|1−x|,x∈(−1,3),where[.] represents greatest integer function.
02:15View Solution∫x02t2[t]dt,where[.] denotes the greatest integer function and x∈R+ , is equal to
02:57View SolutionConsider the function f(x)={x−[x]−12x∉0x∈I where [.] denotes the fractional integral function and I is the set of integers. Then find g(x)max.[x2,f(x),|x|},−2≤x≤2.
04:09View SolutionDiscuss the differentiability of f(x)=[x]+|1−x|,x∈(−1,3),where[.] represents greatest integer function.
05:57View SolutionDiscuss the continuity of the function f(x)={2x−1,ifx<2,3x2,ifx≥2at x=2
02:54View SolutionLet A={x∈R:0≤x≤1}. If f:A→A is defined by f(x)={x,ifx∈Q,1−x,ifx∉Q then prove that fof(x)=x for all x∈A.
07:40View SolutionFind the points of discontinuity of the function: f(x)=[[x]]−[x−1],where[.] represents the greatest integer function
02:45View Solution

