Let denotes the fractional part of are its domain and range, respectively). Then Solution in Tamil
None of these
The correct Answer is:C
is defined if
or
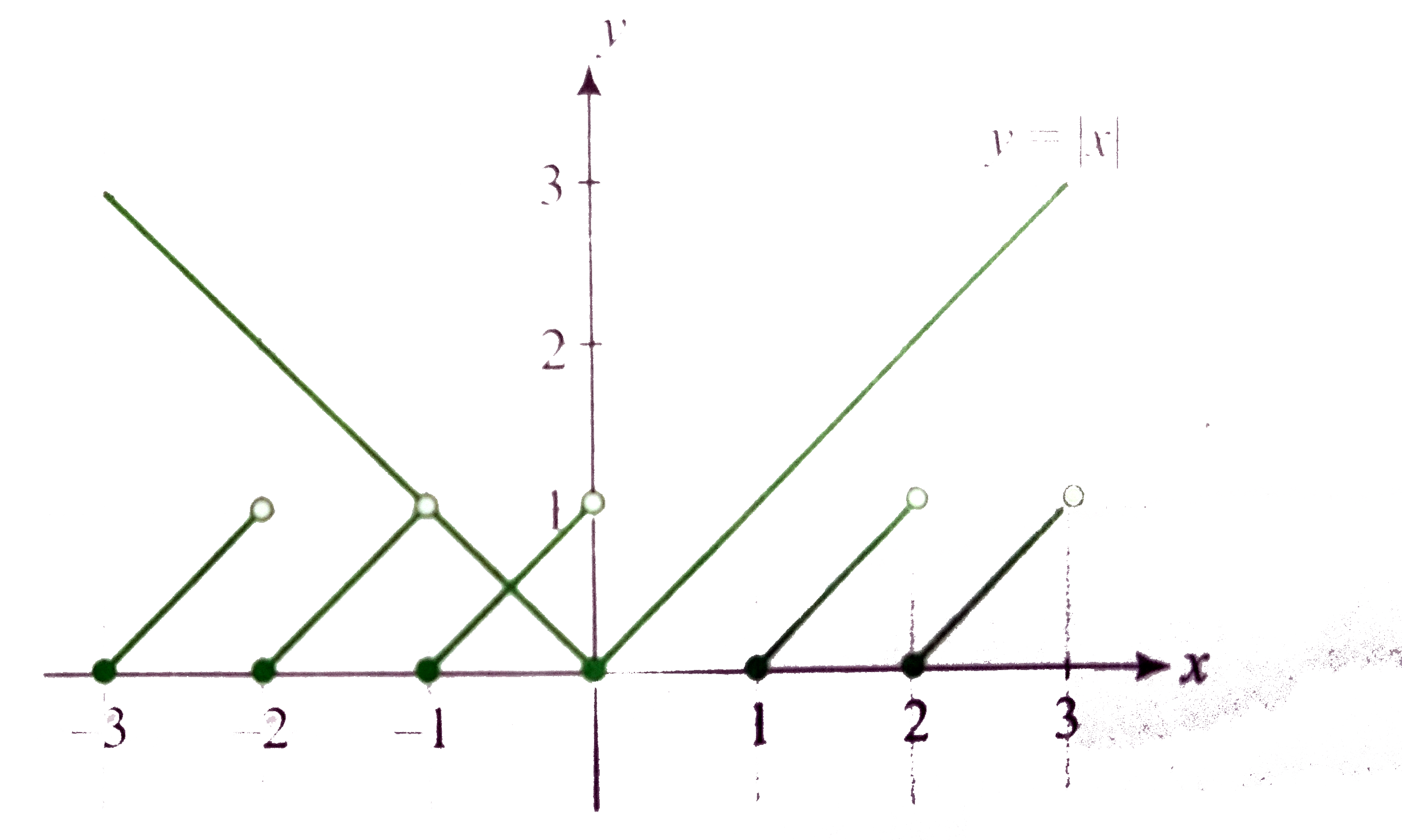
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Multiple)27videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Comprehension)32videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise 1.158videos
RELATIONS AND FUNCTIONS
- BOOK - CENGAGECHAPTER - Quadratic Equations, Inequalities, Modulus and LogarithmsEXERCISE - Question Bank28videos
Quadratic Equations, Inequalities, Modulus and Logarithms
- BOOK - CENGAGECHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.311videos
SCALER TRIPLE PRODUCTS
Similar Questions
Let f(x)=sec−1[1+cos2x], where [.] denotes the greatest integer function. Then the range of f(x) is
02:52View SolutionConsider the functions
f(x)={x+1,x≤12x+1,1<x≤2andg(x)={x2,−1≤x<2x+2,2≤x≤3
The domain of the function f(g(x)) is05:57View SolutionDraw the graph of y=sin|x|.
04:30View SolutionLet a,b,c,d be positive integers such that (log)ab=32and(log)cd=54. If (a−c)=9, then find the value of (b−d).
01:44View SolutionNumber of integral value(s) of λ for which vectors x2ˆi−ˆj+xˆk,(λ−1)ˆi−2λˆj+ˆk and ˆi−ˆj+ˆk, in the order from right-handed system ∀x ∈R, is
03:45View SolutionThe domain of f(x)=log|logx|is (0,∞) (b) (1,∞) (c) (0,1)∪(1,∞) (d) (−∞,1)
02:26View SolutionLet f(x)=√|x|−{x}(where{.} denotes the fractional part of (x)andX,Y are its domain and range, respectively). Then (a) X∈(−∞,12) and Y∈(12,∞) (b)X∈(−∞∈,12)∪[0,∞)andY∈(12,∞) (c)X∈(−∞,−12)∪[0,∞)andY∈[0,∞) (d) none of these
03:08View SolutionThe set of all real numbers x for which x2−|x+2|+x>0 is (−∞,−2) b. (−∞,−√2)∪(√2,∞) c. (−∞,−1)∪(1,∞) d.(√2,∞)
04:36View SolutionThe solution set of the inequality max {1−x2,|x−1|}<1 is (−∞,0)∪(1,∞) (b) (−∞,0)∪(2,∞) (0,2) (d) (0,2)
03:15View SolutionSolution set of the inequation x2+4x+42x2−x−1>0, is x∈(−∞,−2)∪(−2,1) x∈(−∞,−2)∪(−2,−12)∪(1,∞) x∈(−∞,−2)∪(−12,1)∪(1,∞) x∈(−∞,1)
06:12View SolutionSolution set of inequality (ex−1)(2x−3)(x2+x+2)(sinx−2)(x+1)2x≤0 is [32,∞) b. (−∞,−1)∪[32,∞) c. [−1,0)∪[32,∞) d. R−{0,−1}
03:59View SolutionThe set of all real numbers x for which x2−|x+2|+x>0 is (a)(−∞,−2)∪(2,∞) (b) (−∞,−√2)∪(√2,∞) (c)(−∞,−1)∪(1,∞) (d) (√2,∞)
04:38View SolutionThe intervals of increase of f(x) defined by f(x)=∫x−1(t2+2t)(t2−1)dt is equal to (−∞,−32)∪(0,3)∪(10,∞) (−∞, −2)∪(−12,12)∪(4,∞) (−∞, −2)∪(−1,0)∪(1,∞) (−∞, −2)∪(−34,14)∪(1,∞)
04:12View SolutionThe range of (x ^ (2) -2x + 3) / (x ^ (2) -2x-8) AA x in R is (i) (- oo, 0] uu [1, oo) (ii) [ (1) / (2), 2] (iii) (- oo, - (2) / (9)] uu [1, oo) (iv) (oo, -6] uu ([- 2, oo)
03:02View SolutionThe domain of the function f(x)=sin−1(|x|+5x2+1) is
(−∞,−a]∪[a,∞). then a is equal to :03:44View SolutionLet f(x)=√|x|−{x}(where{.} denotes the fractional part of (x)andX,Y are its domain and range, respectively). Then (a) X∈(−∞,12) and Y∈(12,∞) (b)X∈(−∞∈,12)∪[0,∞)andY∈(12,∞) (c)X∈(−∞,−12)∪[0,∞)andY∈[0,∞) (d) none of these
02:51View Solution

