Question

Prove that area common to ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$
and its auxiliary circle $x^2+y^2=a^2$
is equal to the area of another ellipse of semi-axis $aanda-b\stackrel{.}{}$

Explanation

We have ellipse `(x^(2))/(a^(2))+(y^(2))/(b^(2))=1.`
`therefore" "y=pmbsqrt(1-(x^(2))/(a^(2)))`

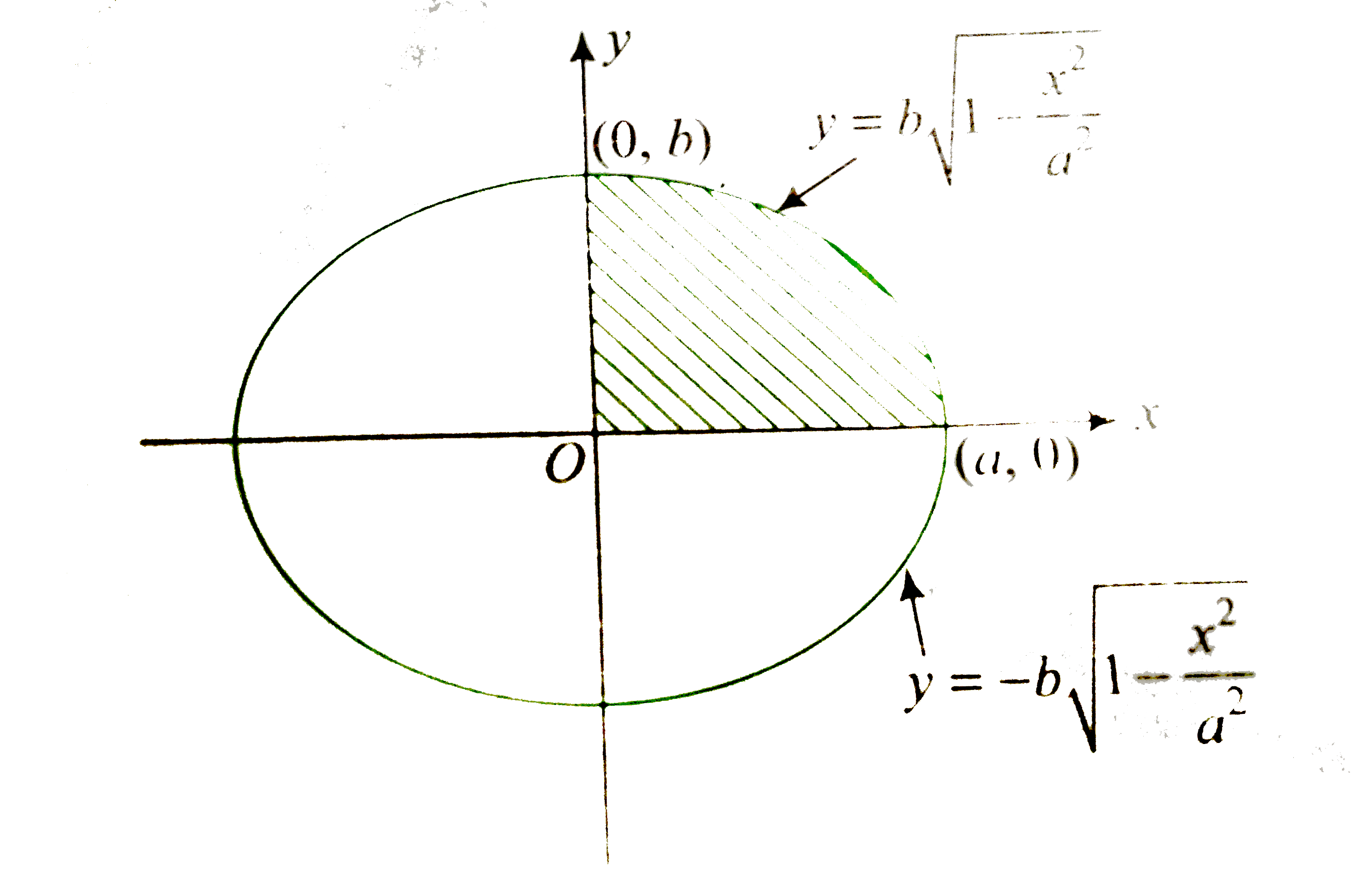
Since graph of the ellipse `(x^(2))/(a^(2))+(y^(2))/(b^(2))=1` is symmetrical about both the axis,
Area enclosed by ellipse `=4xx` Area in the first quadrant
`=4xx overset(a)underset(0)intbsqrt(-1(x^(2))/(a^(2)))dx`
`=(4b)/(a)overset(a)underset(0)intsqrt(a^(2)-x^(2))dx`
`=(4b)/(a)[(x)/(2)sqrt(a^(2)-x^(2))+(a^(2))/(2)sin^(-1)""(x)/(a)]_(0)^(a)`
`=(4b)/(a)[0+(a^(2))/(2)sin^(-1)1-0-0]`
`=(4b)/(2)[(a^(2))/(2)cdot(pi)/(2)]`
`=pi ab`
In the following figure ellipse and its auxiliary are drawn.
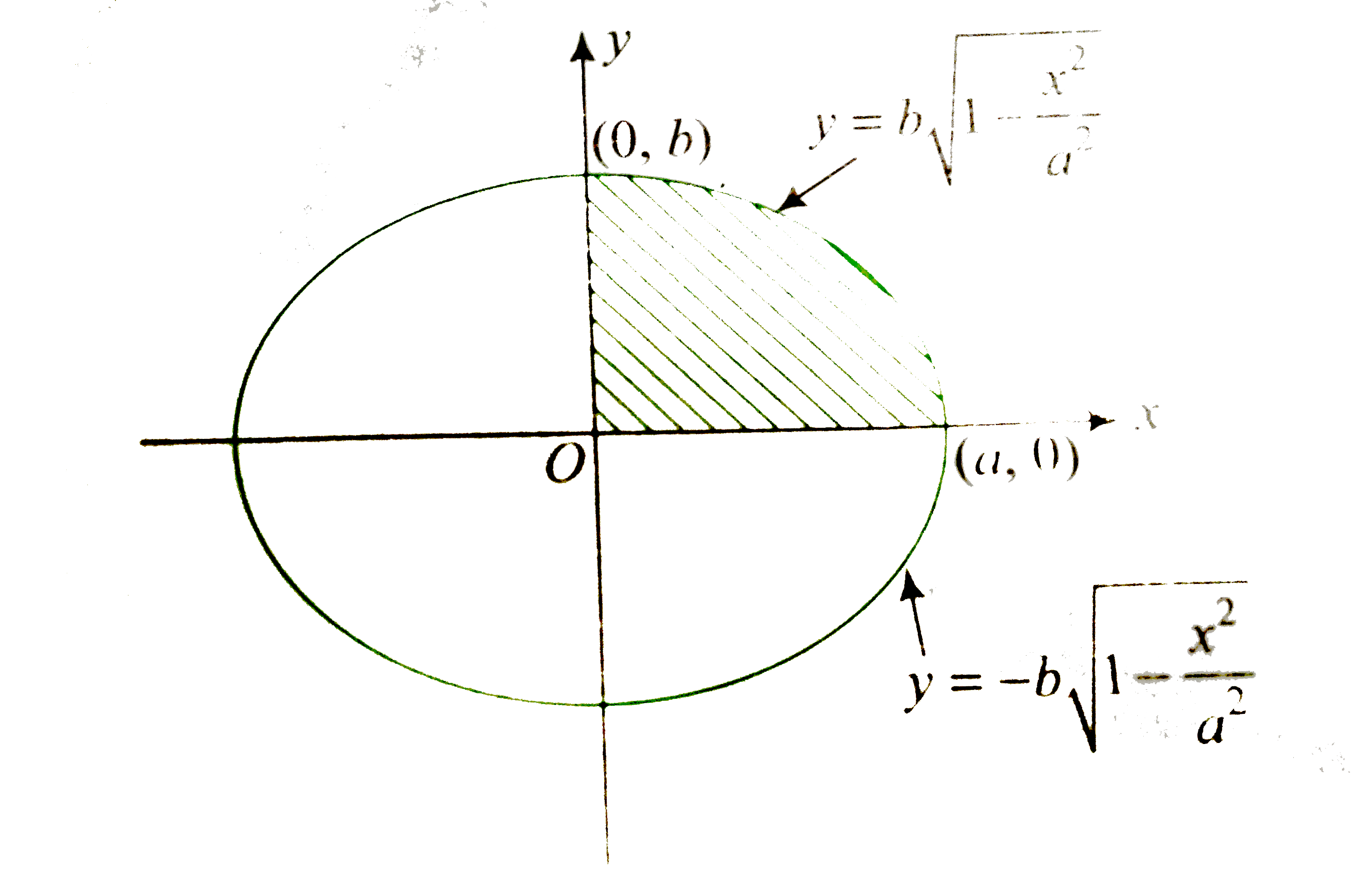ltbvrgt Area of the ellipse `=pi ab`
Area of the circle `=pia^(2)`
Common area between curves is that shown as shaded region
=Area of circle - area of ellipse
`=piab-pia^(2)`
`=pia(b-a)`
This is area of the ellipse whose semi axis are a and (a-b).
One of the possible equations of ellipse is `(x^(2))/(2)+(y^(2))/((a-b)^(2))=1`