Let f(x)= maximum {x2,(1−x)2,2x(1−x)} where x∈[0,1]. Determine the area of the region bounded by the curve y=f(x) and the lines y=0,x=0,x=1.Solution in Tamil
f(x)=Maximum {x2,(1−x2),2x(1−x)}
We draw the graphs of
y=x2 (1)
y=(1−x2) (2)
y=2x(1−x) (3)
Solving (1) and (3), we get x2=2x(1−x)
or 3x2=2x⇒x=0orx=2/3.
Solving (2) and (3) we get (1−x)2=2x(1−x)
⇒ x=1/3andx=1,
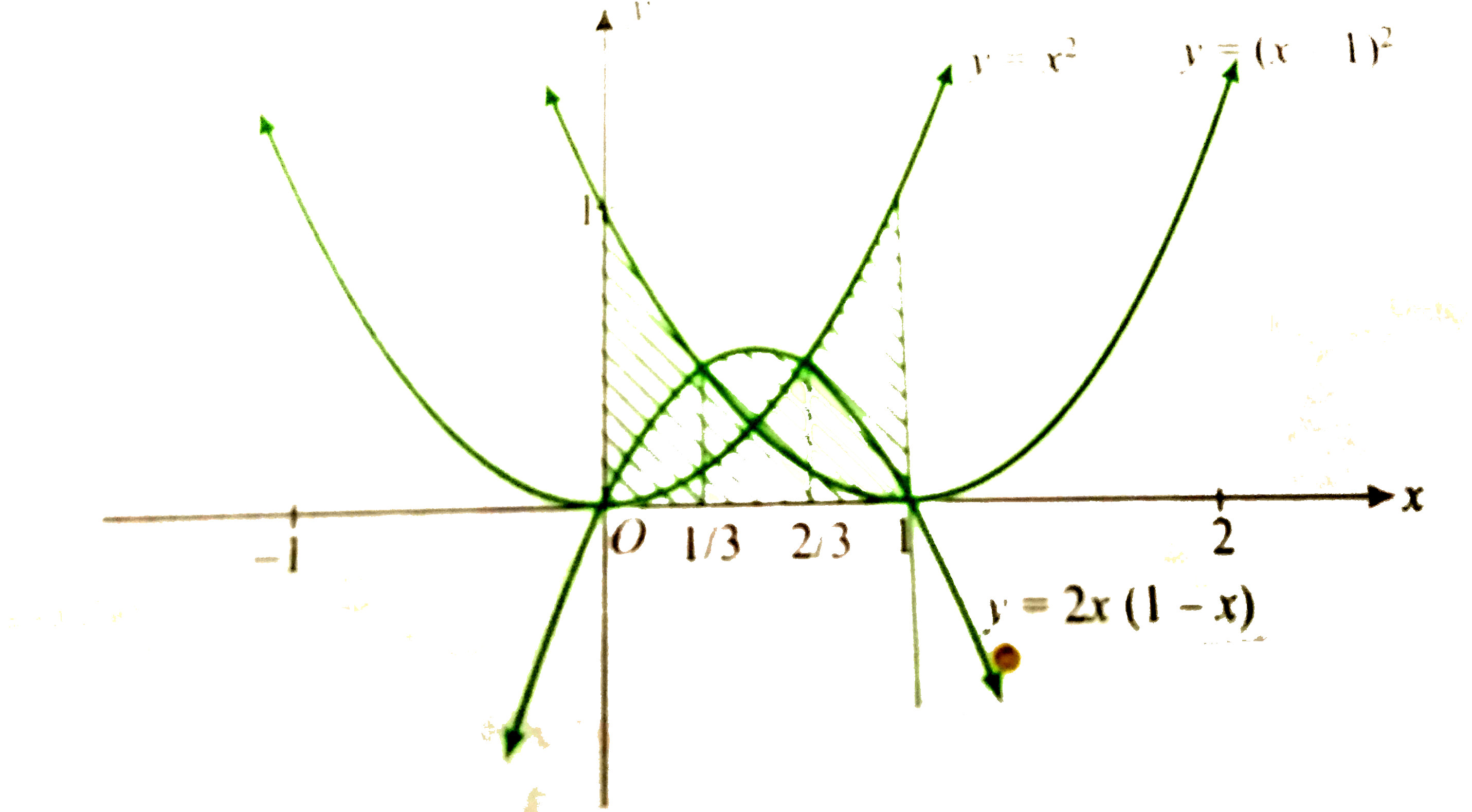
From the figure, it is clear that
f(x)⎧⎪
⎪⎨⎪
⎪⎩(1−x2)for 0≤x≤1/32x(1−x)for 1/3≤x≤2/3x2for 2/3<x≤1
The required area A is given by
A=∫10f(x)dx
=f1/30(1−x)2dx+f2/31/32x(1−x)dx+∫12/3x2dx
=−[13(1−x)3]1/30+[(x2−2x33)]2/31/3+[x33]12/3
=−13(23)3+13+(23)2−23(23)3−(13)2+23(13)3+13−13(23)3
=1727 sq. units.
Topper's Solved these Questions
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.1
9 Videos
- AREABOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.2
14 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type
2 Videos
- AREA UNDER CURVESBOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank
10 Videos
Similar Questions
Find the area of the smaller part of the circle x2+y2=a2 cut off by the line x=a√2.
View SolutionFind the area lying in the first quadrant and bounded by the curve y=x3 and the line y=4x.
View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
View SolutionThe area of the region (s) enclosed by the curves y=x2 and y=√|x| is
View SolutionLet F(x)=int_(x)^(x^(2)+(pi)/(6))[2cos^(2)t.dt] for all x in R and f:[0,(1)/(2)]rarr[0,oo) be a continuous function.For a in[0,(1)/(2)], if F'(a)+2 is the area of the region bounded by x=0,y=0 is the area x=a, then f(0) is
View SolutionLet f(x)= maximum {x^(2),(1-x)^(2),2x(1-x)} where0<=x<=1 The area of the region bounded by the curves y=f(x), x-axes,x=0 and x=1 is
View SolutionLet f(x)= maximum {x^(2),(1-x)^(2),2x(1-x)} where x in[0,1] . Determine the area of the region bounded by the curve y=f(x) and the lines y=0,x=0,x=1
View SolutionIf a curve y=f(x) satisfies y''x^(2)+x(y')^(2)=2xy',f(0)=0 and f'(1)=1 then f(x) is
View SolutionFind the area of the region bounded by the curves y=√x+2andy=1x+1 between the lines x=0 and x=2.
View SolutionThe area of the region bounded by the curves 2x=y2−1 and x=0
View SolutionThe area of the region bounded by the curves y=2x,y=2x−x2 and the lines x=0,x=2 is
View SolutionThe area bounded between the curves y=f(x) , y=g(x)where f(x)=x3 and g(x)={x5if−1≤x≤0xif0≤x≤1 is
View SolutionLet f(x)= max {x2,(1−x)2,2x(1−x)} where 0≤x≤1. Determine the area of the region bounded by y=f(x), x-axis, x = 0 and x = 1.
View SolutionThe area of the region bounded by curves y=1−x2,x+y+1=0andx−y−1=0 is
View SolutionLet f(x)= maximum {x2,(1−x)2,2x(1−x)} where x∈[0,1]. Determine the area of the region bounded by the curve y=f(x) and the lines y=0,x=0,x=1.
View Solution
