Find the area bounded by the curve f(x)=x+sinxand its inverse function between the ordinates x=0 to x=2π.Solution in Tamil
y=x+sinx
∴ dydx=1+osx≥0∀x
Also d2ydx2=−sinx=0 when x=nπ,n∈Z
Hence x=nπ are points of inflection, where curve changes its concavity.
Also, for x∈(0,π),sinx>0⇒x+sinx>x
And for x∈(π,2π),sinx<0⇒x+sinx<x
Thus, we have following graphs of function y=f(x) and its inverse function.
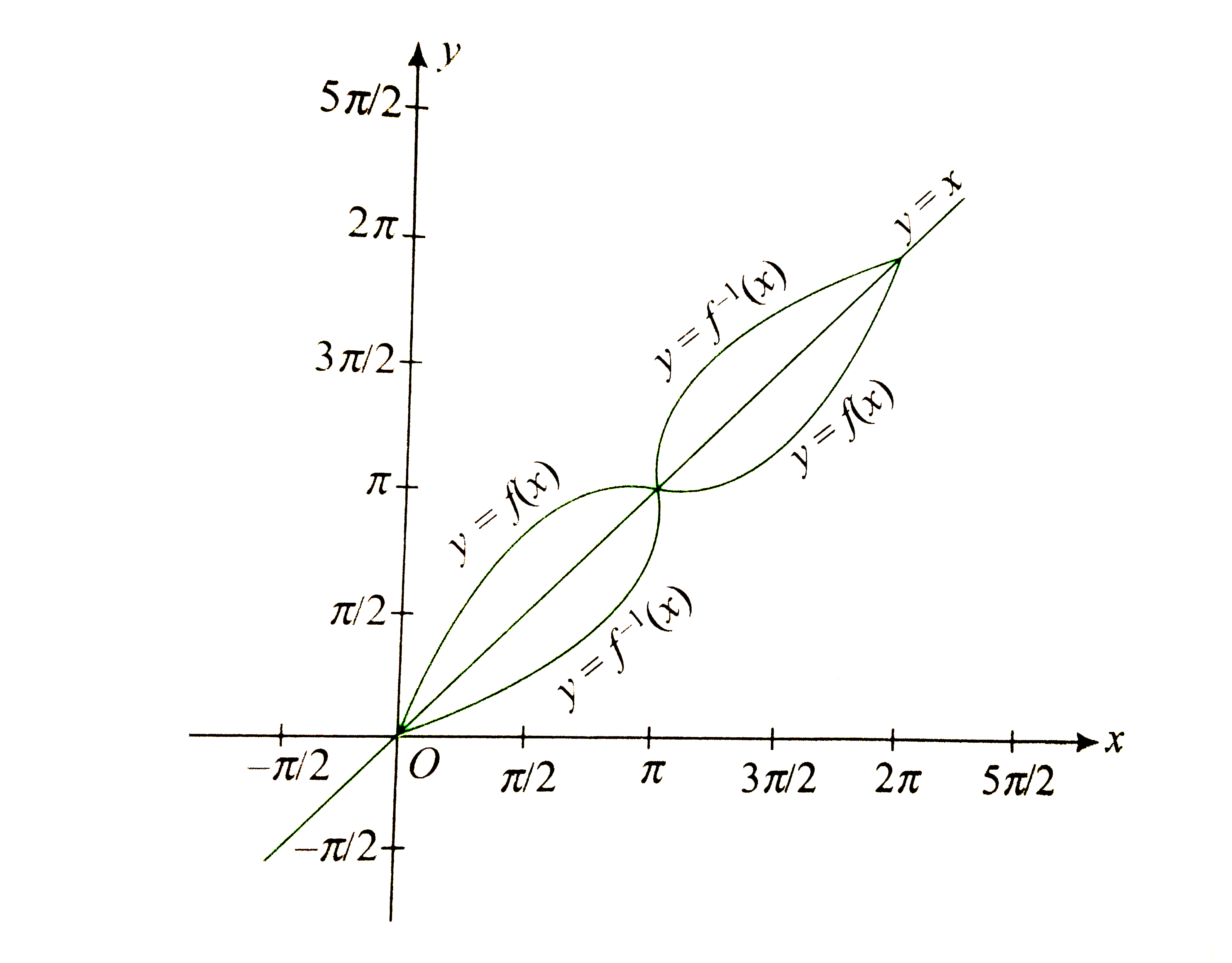
Required area =4∫π0(f(x)−x)dx
=4∫π0sinxdx=4×2=8 sq. units.
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.19videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.214videos
AREA
- BOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type2videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank10videos
AREA UNDER CURVES
Similar Questions
Find the area of the smaller part of the circle x2+y2=a2 cut off by the line x=a√2.
02:22View SolutionFind the area lying in the first quadrant and bounded by the curve y=x3 and the line y=4x.
01:48View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
09:40View SolutionThe area of the region (s) enclosed by the curves y=x2 and y=√|x| is
03:32View SolutionFind the area bounded by the curve f(x)=x+sinxand its inverse function between the ordinates x=0 to x=2π.
03:16View SolutionFind the area of the region bounded by the curve y=sinx between x=0andx=2π.
04:28View SolutionFind the area of the region bounded by the curve y=cosx,xaxis and the ordinates x=0 and x=2π
03:50View SolutionThe area (in square unit) bounded by the curve y= sin x, x-axis and the two ordinates x =π,x=2π is-
01:31View SolutionThe area bounded by the curves y=cos x and y=sin x between the ordinates x=0 and x=3/2pi is :
03:20View SolutionFind the area bounded by the curve y = sin x between x = 0 and x = 2π.
03:52View SolutionFind the area bounded by the curve y = sin x between x = 0 and x=2π.
04:55View SolutionFind the area bounded by the curve y = sin x between x = 0 and x=2π.
02:47View SolutionFind the area bounded by the curve f(x)=x+sinxand its inverse function between the ordinates x=0 to x=2π.
04:06View SolutionFind the area bounded by the curve y = sin x between x = 0 and x=2π.
04:42View SolutionThe area of the region bounded by the curve y=sinx, x-axis in [0,2π] is
05:21View Solution

