Let An be the area bounded by the curve y=(tanx)n and the lines x=0,y=0, and x=π4. Prove that for n>2,An+An−2=1n−1 and deduce 12n+2<An<12n−2Solution in Tamil
We have An=∫π/40(tanx)ndx
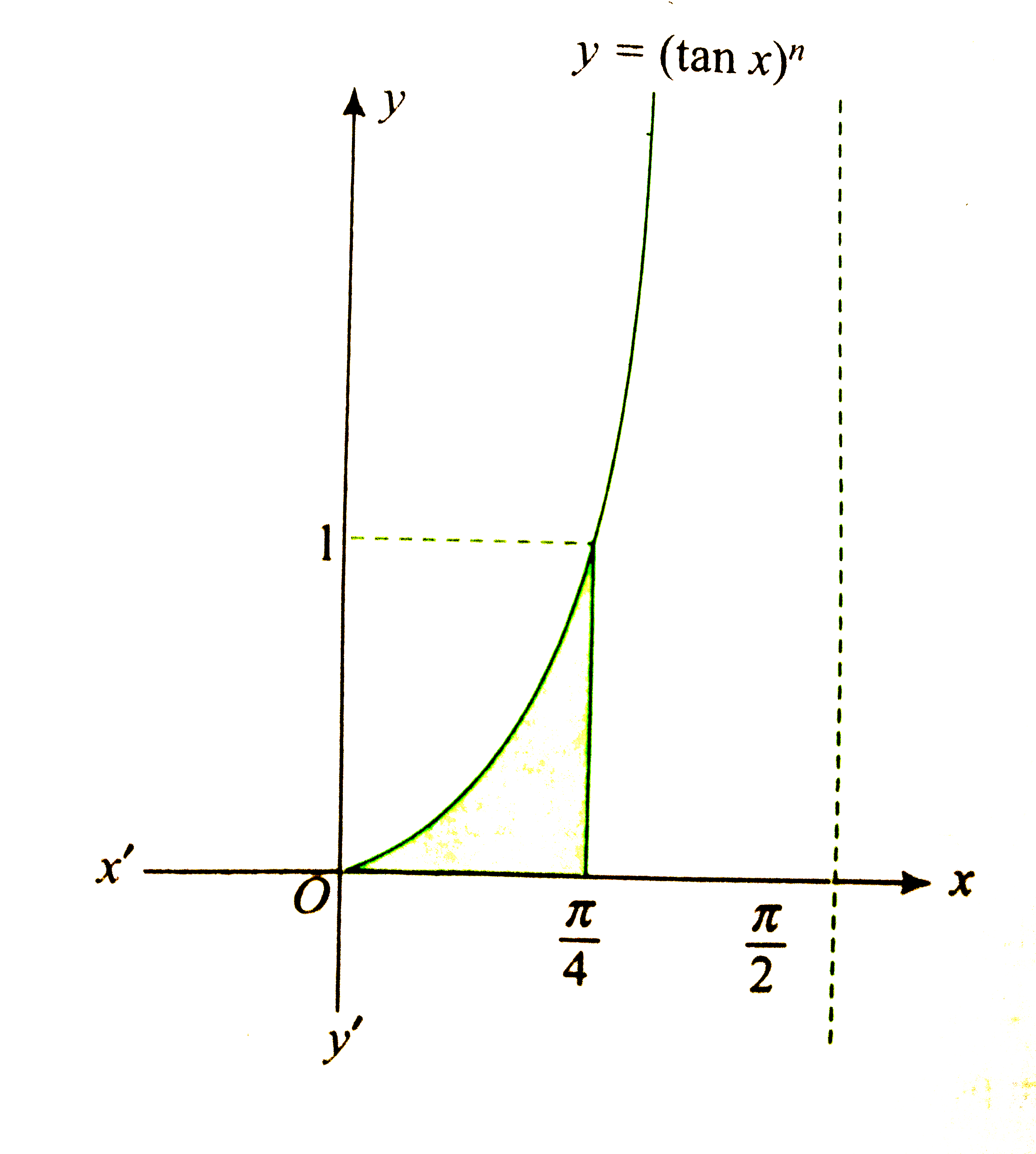
Since 0<tnax<1, when 0<x<π/4, we have
0<(tanx)n+1<(tanx)n for each n∈N
⇒ ∫π/40(tanx)n+1dx<∫π/40(tanx)ndx
⇒ An+1<An
Now, for n>2,
An+An+2=∫π/40[(tanx)n+(tanx)n+2]dx
=∫π/40(tanx)n(1+tan2x)dx
=∫π/40(tanx)n(sec2x)dx
=[1(n+1)(tanx)n+1]π/40
[∵∫[f(x)]nf'(x)dx=[f(x)]n+1n+1]
=1(n+1)(1−0)
Since An+2<An+1<An, we get
An+An+2<2An
⇒ 1n+1<2An⇒12n+2<An (1)
Also for n>2,An+An<An+An−2=1n−1
or 2An<1n−1
or An<12n−2 (2)
Combining (1) and (2), we get 12n+2<An<12n−2.
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.19videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.214videos
AREA
- BOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type2videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank10videos
AREA UNDER CURVES
Similar Questions
Find the area of the smaller part of the circle x2+y2=a2 cut off by the line x=a√2.
07:34View SolutionFind the area lying in the first quadrant and bounded by the curve y=x3 and the line y=4x.
06:43View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
07:23View SolutionThe area of the region (s) enclosed by the curves y=x2 and y=√|x| is
03:40View SolutionIf An=∫π20sin(2n−1)xs∈xdx;Bn=∫pi20(s i n n xs∈x)2dx;f o rn∈N,t h e n An+1−An b. Bn+1−Bn c. An+1−An=Bn+1 d. Bn+1−Bn=An+1
02:30View SolutionLet {a_n} be a non-constant arithmetic progression a_1 =1 and a_(2n+a_(2n-1)+....+a_(n+1))/(a_n+a_(n-1)+....+a_1) remains constant (for n leq 1).Then a_15 is
06:15View SolutionIf An be the area bounded by the curve y=(tanxn) ands the lines x=0, y=0, x=π/4 Prove that for n>2. , An+An+2=1n+1 and deduce 12n+2<An<12n−2
06:50View Solution{an}and{bn} are two sequences given by an=(x)1/2n+(y)1/2nandbn=(x)1/2n−(y)1/2n for all n ∈ N. The value of a1a2a3……..an is equal to
12:06View SolutionA sequence of numbers An,n=1,2,3 is defined as follows : A1=12 and for each n≥2, An=(2n−32n)An−1 , then prove that n∑k=1Ak<1,n≥1
02:43View SolutionIf a1,a2,a3,,a2n+1 are in A.P., then a2n+1−a1a2n+1+a1+a2n−a2a2n+a2++an+2−anan+2+an is equal to a. n(n+1)2×a2−a1an+1 b. n(n+1)2 c. (n+1)(a2−a1) d. none of these
07:36View SolutionIf An be the area bounded by the curve y=(tanx)n and the lines x=0, y=0, x=π/4 , then for n>2.
03:52View SolutionWrite the first five terms of each of the following sequences whose n th terms are: an=3n+2 (ii) an=n−23 an=3n (iv) an=3n−25 an=(−1)n.2n (vi) an=n(n−2)2 (vii)an=n2−n+1 (viii) an=2n2−3n+1 (ix)an=2n−36
03:52View SolutionLet a sequence be defined by a1=1,a2=1 and an=an−1+an−2 for all n>2, Find an+1an for n=1,2,3,4.
04:06View SolutionGiven a1=12(a0+Aa0),a2=12(a1+Aa1) and an+1=12(an+Aan) for n≥2, where a>0,A>0. prove that an−√Aan+√A=(a1−√Aa1+√A)2n−1.
05:47View Solutionमाना वक्र y=xn(n≥1) एवं रेखा x=0,y=0 एवं x=12 द्वारा परिबर क्षेत्रफल An है। यदि n∑n=12nAnn=13 है, तो n का मान ज्ञात कीजिये।
06:21View Solution

