Find the area bounded by the curve xy2=4(2−x) and y-axis.Solution in Tamil
The correct Answer is:4π sq. units
We have curve xy2=4(2−x)
∴ x=8y2+4
The given curve is symmetrical about x-axis and meets it at (2,0).
Also, when y→±∞,x→0.
So, y-axis is asymptote to the curve.
The graph of the function is as shown in the following figure.
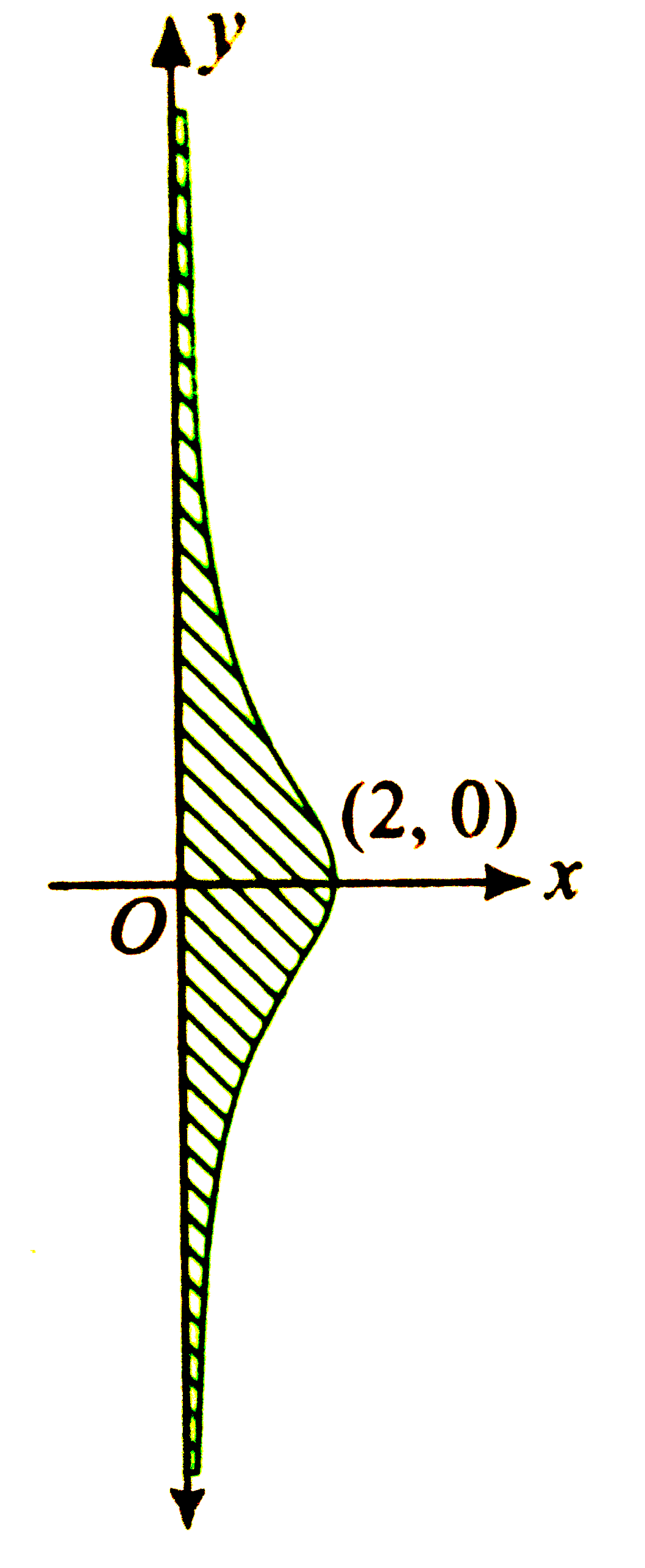
The line x=0, i.e., y-axis is asymptote.
Area of the shaded region =2∫∞08y2+4dx
=16[12tan−1y2]∞0=8×π2
=4π sq. units
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.214videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.37videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Comprehension Type2videos
AREA
- BOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type2videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank10videos
AREA UNDER CURVES
Similar Questions
Find the area lying in the first quadrant and bounded by the curve y=x3 and the line y=4x.
04:10View SolutionFind the continuous function f where (x4−4x2)≤f(x)≤(2x2−x3) such that the area bounded by y=f(x),y=x4−4x2. then y-axis, and the line x=t, where (0≤t≤2) is k times the area bounded by y=f(x),y=2x2−x3,y−aξs, and line x=t(where0≤t≤2).
02:50View SolutionIn the following figure, the graphs of two functions y = f(x) and y = sin x are givne. They intersect at origin, A(a,f(a)),B(π,0)andC(2π,0).Ai(i=1,2,3) is the area bounded by the curves as shown in the figure, respectively, for x∈(0,a),x∈(a,π),x∈(π,2π).
If A1=1+(a−1)cosa−sin a, then

The function f(x) is04:28View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
04:16View SolutionThe area of the region (s) enclosed by the curves y=x2 and y=√|x| is
03:13View SolutionFind the area bounded by the curves y=x+sqrt(x^(2)) and xy=1, the x -axis and the line x=2
View SolutionFind the area bounded by the curve xy2=4(2−x) and y-axis.
View Solutionप्रथम चतुर्थांश में वक्र y2=9x,x=2,x=4 एवं x -अक्ष से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए|
05:02View SolutionArea bounded by the curve xy^(2) = a^(2) (a -x) and y-axis is
09:39View Solutionप्रथम चतुर्थाश में वक्र y2=9x,x=2,x=4 एव X -अक्ष से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
04:41View Solutionवक्र xy2=a2(a−x) और y- अक्ष से परिबद्ध क्षेत्रफल ज्ञात कीजिए।
03:15View Solutionवक्र y=4−x2,x अक्ष तथा x=2 से परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
05:02View Solutionवक्र xy2=a2(a−x) एवं y- अक्ष से घिरे क्षेत्र का क्षेत्रफल होगा
03:09View Solutionवक्र xy2=a2(a−x) एवं Y-अक्ष द्वारा परिबद्ध क्षेत्र के क्षेत्रफल का आधा है
08:42View Solutionवक्र xy2=4(2−x) तथा Y- अक्ष से घिरे क्षेत्र का क्षेत्रफल है
02:35View Solution

