Area bounded by the curve xy2=a2(a−x) and the y-axis is πa22sq.units (b) πa2sq.units (c) 3πa2sq.units (d) None of theseSolution in Tamil
4a2 sq. units
8a215 sq. units
16a29 sq. units
None of these
The correct Answer is:B
ay2=x2(a−x)ory=±x√a−xa
Curve tracing : y=x√a−xa
We must have x≤a
For 0<x≤a,y>0and for x<0,y<0
Also y=0⇒x=0,a
Curve is symmetrical about x-axis.
When x→−∞,y→−∞
Also, it can be verified that y has only one point of maxima for 0<x<a.
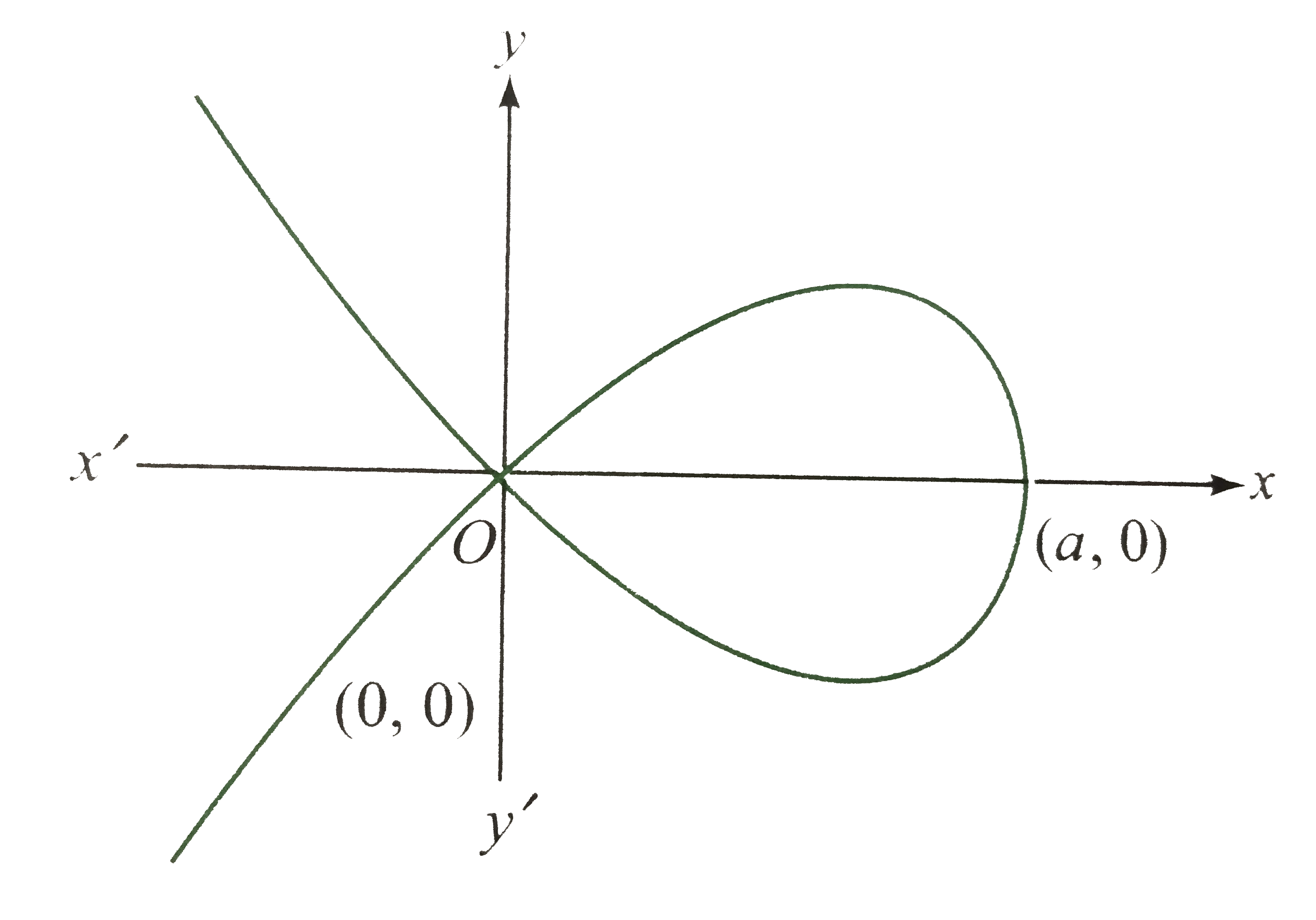
Area =2a∫0x√a−xadx
√a−xa=t
⇒ 1−xa=t2orx=a(1−t2)
⇒ A=20∫1a(1−t2)t(−2at)dt
4a21∫0(t2−t4)dt
=4a2[t33−t55]10
=4a2[13−15]
=8a215 sq. units.
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Multiple)10videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Comprehension)21videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.37videos
AREA
- BOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type2videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank10videos
AREA UNDER CURVES
Similar Questions
Let A(k) be the area bounded by the curves y=x2−3 and y=kx+2 The range of A(k) is (10√53,∞) The range of A(k) is (20√53,∞) If function k→A(k) is defined for k∈[−2,∞ ), then A(k) is many-one function. The value of k for which area is minimum is 1.
11:48View SolutionLet Ar be the area of the region bounded between the curves y2=(e−kr)x(where k>0,r∈N) and the line y=mx(where m≠0), k and m are some constants
A1,A2,A3,… are in G.P. with common ratio06:08View SolutionFind the continuous function f where (x4−4x2)≤f(x)≤(2x2−x3) such that the area bounded by y=f(x),y=x4−4x2. then y-axis, and the line x=t, where (0≤t≤2) is k times the area bounded by y=f(x),y=2x2−x3,y−aξs, and line x=t(where0≤t≤2).
06:31View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
06:05View SolutionThe area of the region (s) enclosed by the curves y=x2 and y=√|x| is
08:39View SolutionThe area enclosed between the curves y=(log)e(x+e),x=(log)e(1y), and the x-axis is 2sq.units (b) 1sq.units 4sq.units (d) none of these
12:16View SolutionThe area of the region bounded by x=0,y=0,x=2,y=2,y≤exandy≥1nx is 6−41n2sq.units (b) 41n2−2sq.units 21n2−4sq.units (d) 6−21n2sq.units
04:17View SolutionIf f(x)=sinx,∀x∈[0,π2],f(x)+f(π−x)=2,∀x∈(π2,π)andf(x)=f(2π−x),∀x∈(π,2π), then the area enclosed by y=f(x) and the x-axis is πsq.units (b) 2πsq.units 2sq.units (d) 4sq.units
06:10View SolutionThe area of the region enclosed between the curves x=y2−1andx=|y|√1−y2 is 1sq.units (b) 43sq.units 23sq.units (d) 2sq.units
04:34View SolutionThe area of the closed figure bounded by x=−1,x=2,and y={−x2+2,x≤12x−1,x>1andtheabscissaaξsis 163sq.units (b) 103sq.units 133sq.units (d) 73sq.units
03:35View SolutionThe area enclosed between the curves y=(log)e(x+e),x=(log)e(1y), and the x-axis is (a) 2sq.units (b) 1sq.units (c) 4sq.units (d) none of these
04:30View SolutionThe area enclosed between the curve y2(2a−x)=x3 and the line x=2a above the x-axis is (a) πa2sq.units (b) 3πa22sq.units (c) 2πa2sq.units (d) 3πa2sq.units
05:57View SolutionA particle of mass m is moving anticlockwise, in a circle of radius R in x−y plane with centre at (R,0) with a constant speed v2. If is located at point (2R,0) at time t=0. A man starts moving with a velocity v1 along the positive y-axis from origin at t=0. Calculate the linear momentum of the particle w.r.t. man as a function of time.
05:09View SolutionThe area of the smaller region bounded by circle x2+y2=1 and |y|=x+1 (a)π2−12sq.units (b) π2−1sq.units (c) π2sq.units (d) π2+1sq.units
05:06View SolutionThe area of the closed figure bounded by y=x22−2x+2 and the tangents to it at (1,12)and(4,2) is 98sq.units (b) 38sq.units 32sq.units (d) 94sq.units
07:49View SolutionThe area of the loop of the curve ay2=x2(a−x) is 4a2sq.units (b) 8a215sq.units 16a29sq.units (d) None of these
05:26View Solution

